补充
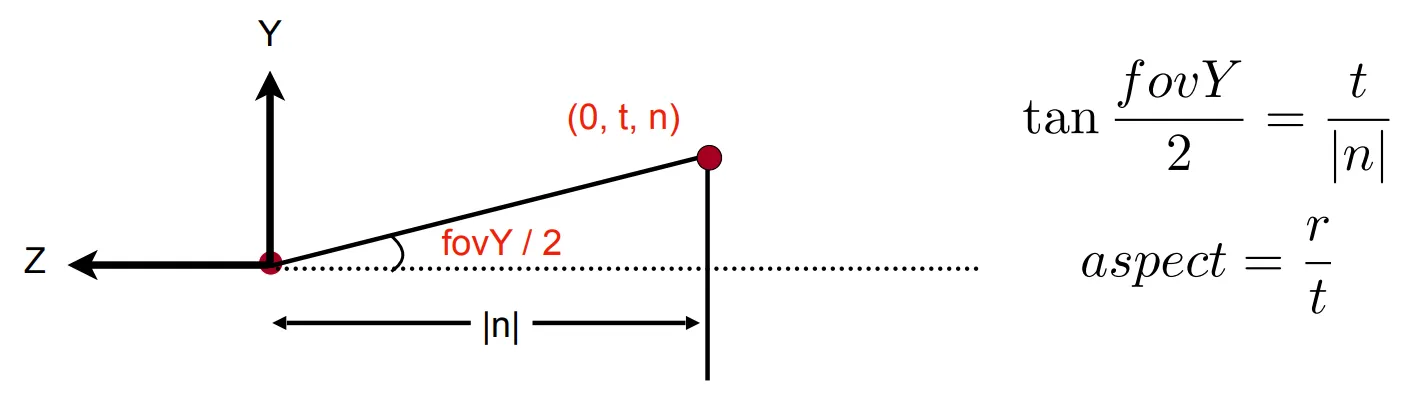
field-of-view(fovY) 和 aspect ratio(可以认为, l=-r, b=-t)

为什么需要这两个概念呢?
因为通过这两个概念可以帮助我们求得 l, r, b, t 的值
光栅化
简单地说,光栅化的过程就是将想要展现的物体给真正显示到屏幕上的过程,因为我们的物体其实都是一个个顶点数据,如何将表达这些蕴含几何信息的数据转化为屏幕上的像素就是光栅化需要考虑的东西。比如说一条直线,究竟该用哪些点去逼近它,一个三角形,又该用哪些像素集合表示它,这都是光栅化的过程。
在正式开始介绍光栅化之前,我们先补充一些基本概念。
屏幕
像素矩阵,1920 * 1020等等
数组大小: 分辨率
典型的栅格显示
栅格
德语中屏幕的意思
栅格化,画在屏幕上
像素
"picture element"的缩写
到目前为止,我们先简单的认为像素就是一个具有单一颜色的小矩形
颜色是红,绿,蓝的混合
屏幕中像素的表示
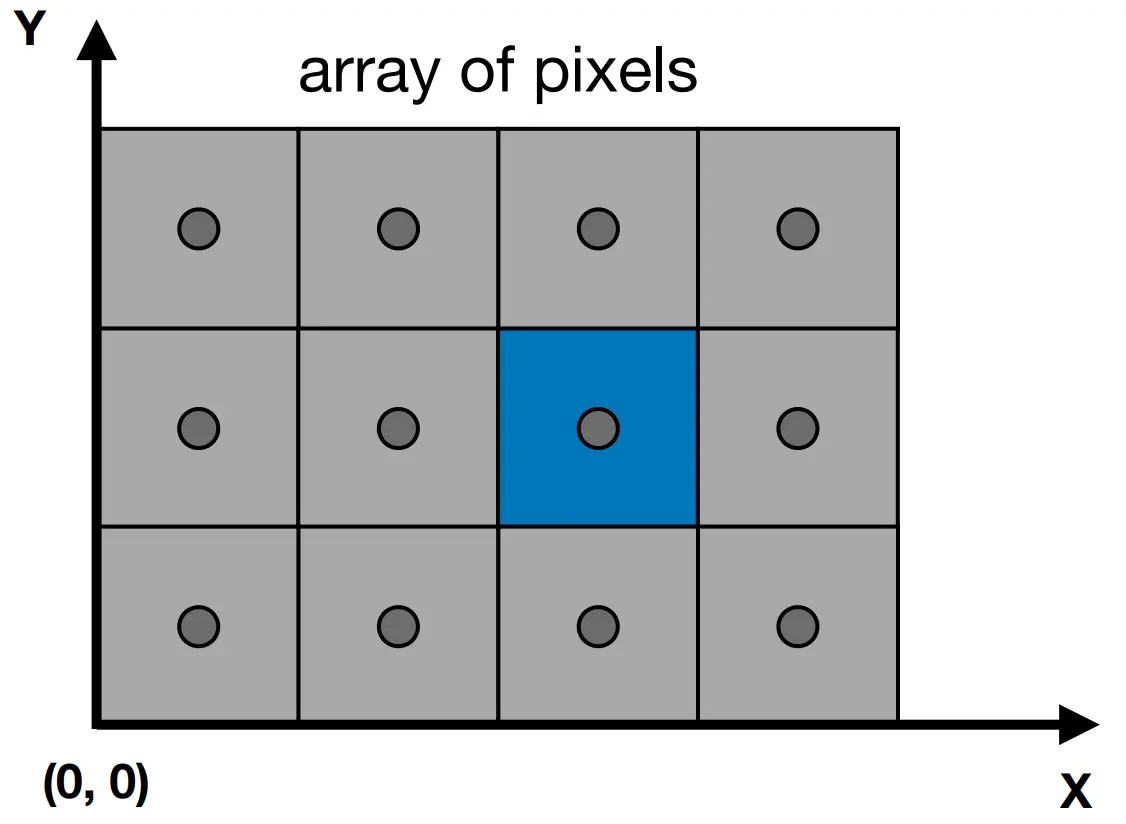
每个像素都用屏幕中的坐标来进行表示,例如图中蓝色像素,可以用(2, 1)来进行表示。同时,因为每个像素都有一定的面积,所以使用(x+0.5, y+0.5)来表示(x, y)像素的中心。
视口变换
当我们得到[-1, 1]^3的立方体时,我们需要将其转换成屏幕大小,这个变换就叫做视口变换。
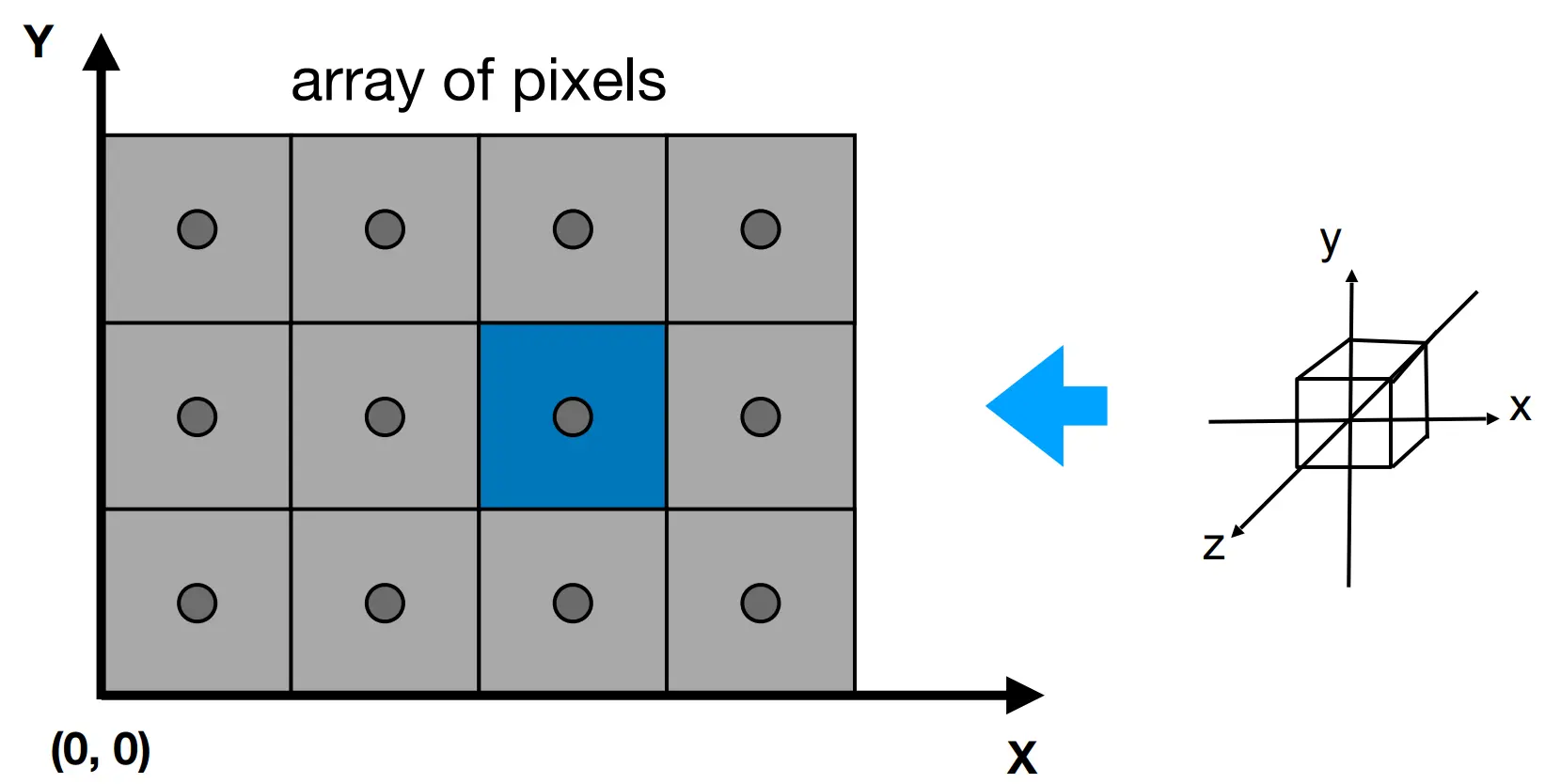
先不考虑z坐标
xy平面中的变换:[-1, 1]^2到[0, width] \times [0, height]
变换矩阵
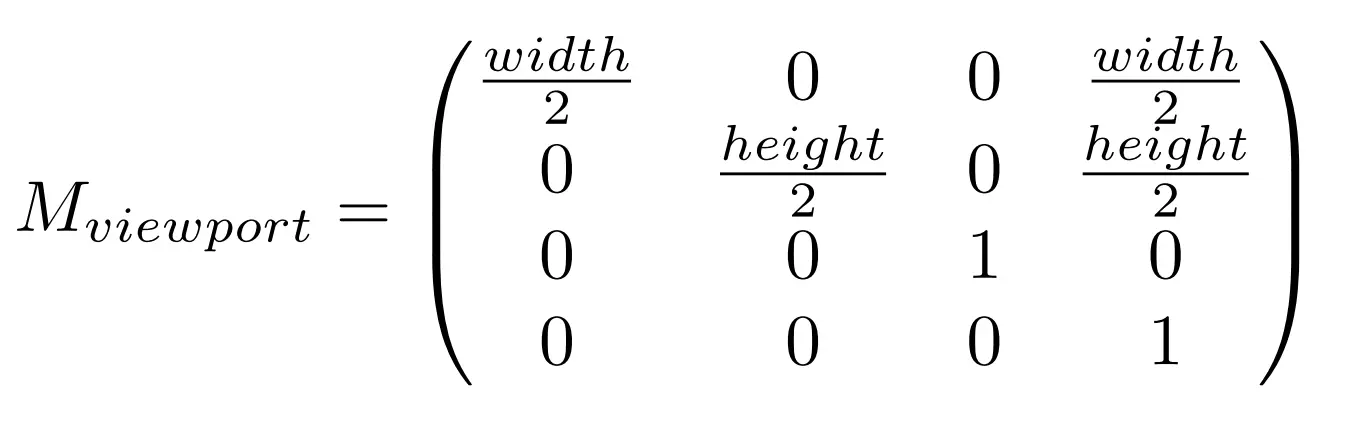
三角光栅化算法
为什么选择三角形呢?
最基本的多边形
任何多边形,都可以划分成三角形
独一无二的性质:
三角形一定保证在一个平面内
能很清晰的定义出三角形的内部和外部
很容易计算出一个点是位于三角形内部还是外部(通过叉乘)
只要定义出三角形的三个顶点的属性,那三角形内部的任意一点都能通过插值的方式计算出对应的属性(通过重心坐标进行插值)
首先,我们需要先进行采样
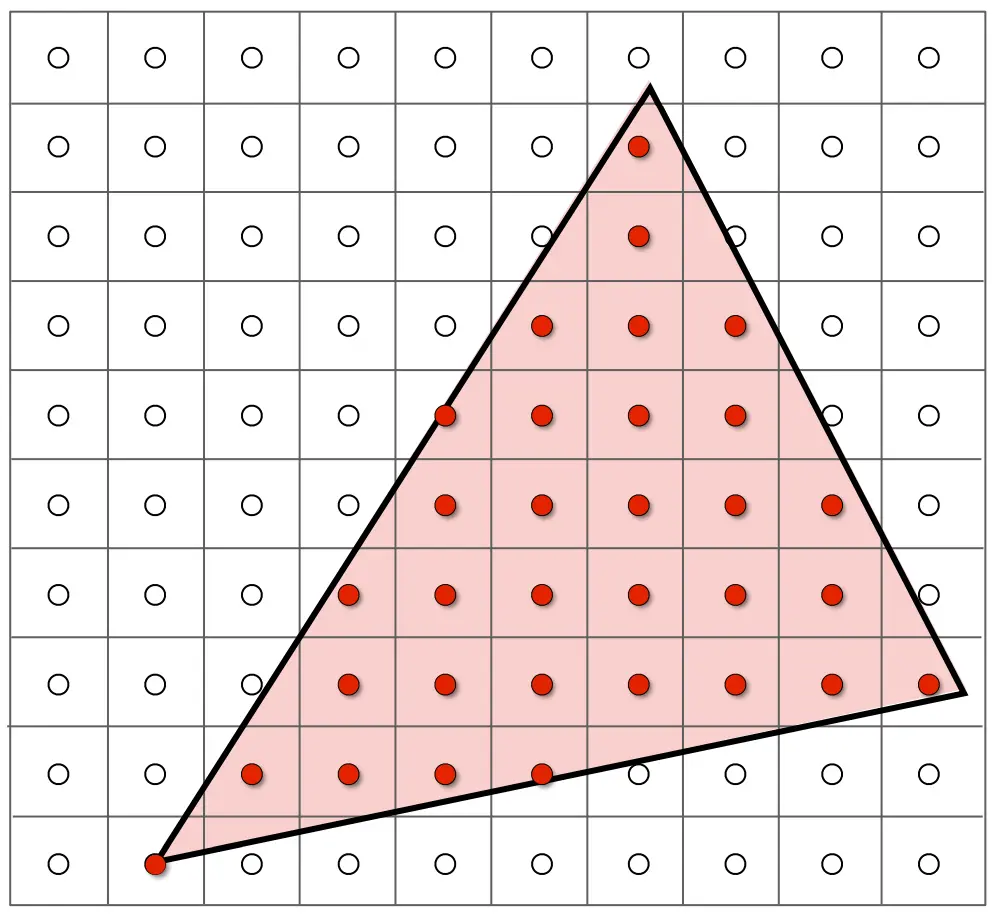
我们简单地通过像素的中心来进行判断,如果像素的中心在三角形内,则认为该像素在三角形内。在本课程中,如果中心在边界,则认为该像素不在三角形内部。
如何判断点是否在三角形内部呢?
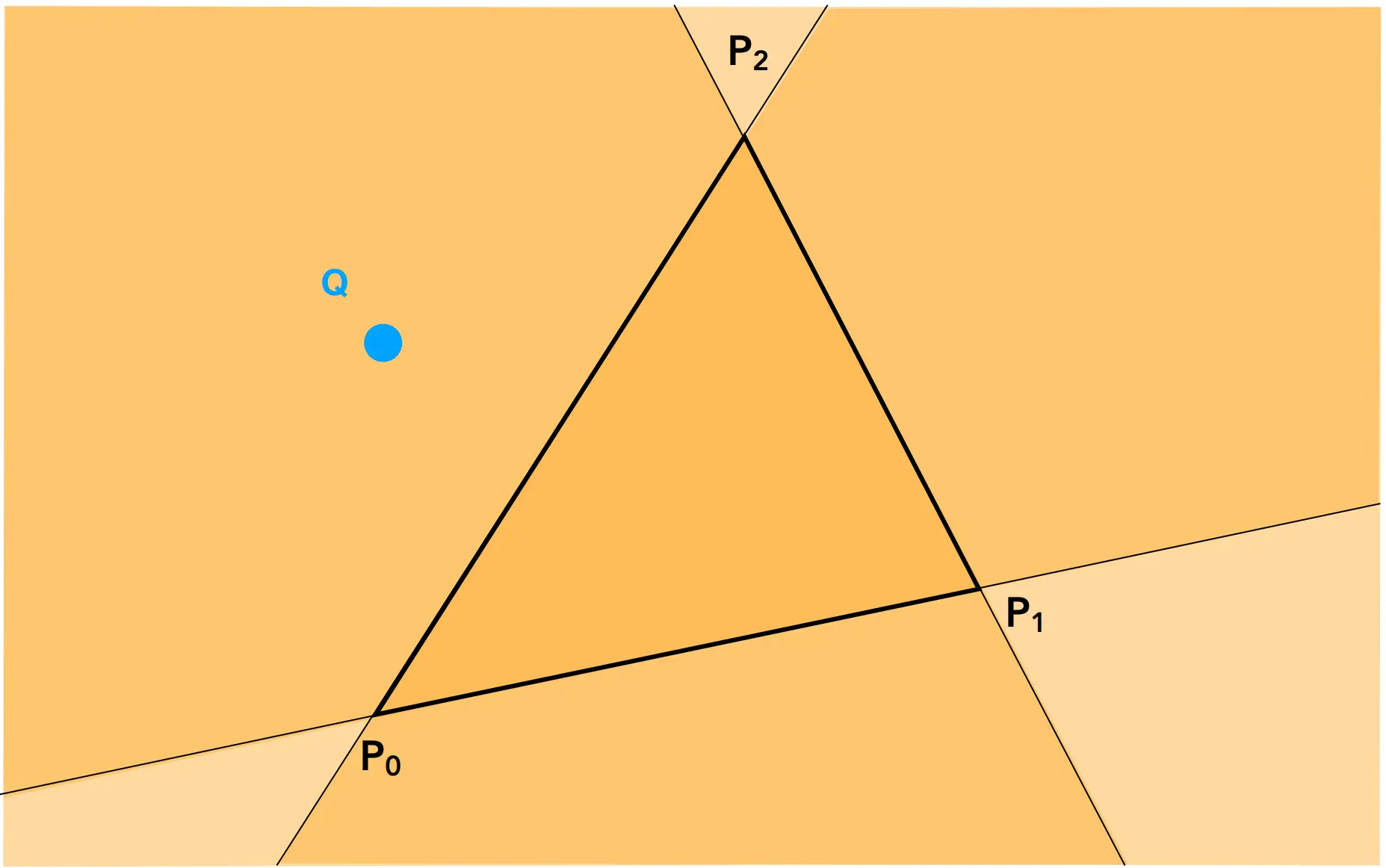
通过叉乘就可以得到,对于点 Q,我们需要计算P_0P_1 \times P_0Q,P_1P_2 \times P_1Q,P_2P_0 \times P_2Q,如果三者同号则代表点 Q 在三角形内部,如果不同号,则代表在三角形外部。
因此,我们遍历每个像素点来计算是否在三角形内部即可。但是我们可以进一步优化,利用一个 bouding box 包围住想要测试的三角形。
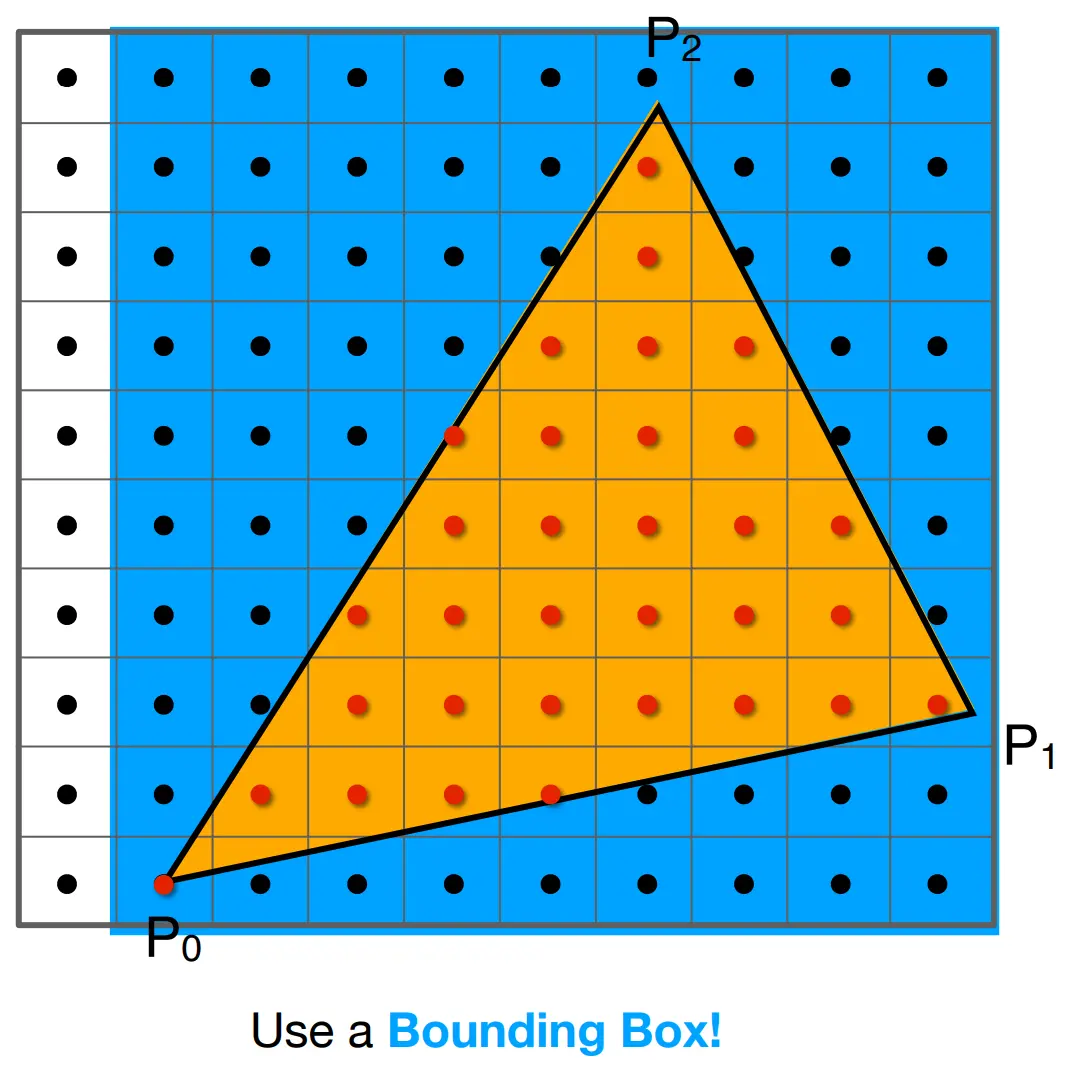
但是,在填充之后,会得到如下图所示的结果,显然不是特别理想。在后面,我们会进一步去优化。