画家算法（Painter's Algorithm）

从后到前绘制，覆盖帧缓冲区

不同的绘制顺序，可能会产生不同的结果

此外，需要对深度进行排序（n 个三角形需要 O(nlogn)），存在无法解决的深度值顺序问题

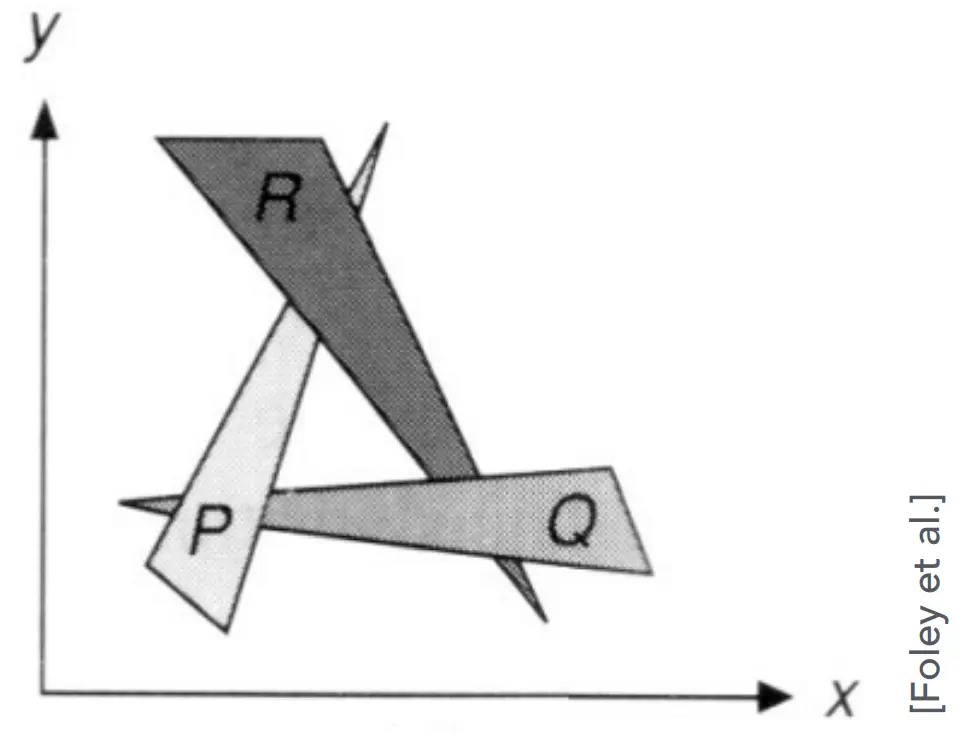
Z-Buffer

介绍

• 存储每个采样点（像素）当前的 min z-value

• 需要额外的 buffer 存储深度值

  • frame buffer 存储 color values

  • depth buffer（z-buffer）存储 depth

主要点：为了简化理解，我们假设 z 总是正数（z 越小，表示越近，z越大，表示越远）

伪代码

同时更新 framebuffer 和 zbuffer

例子

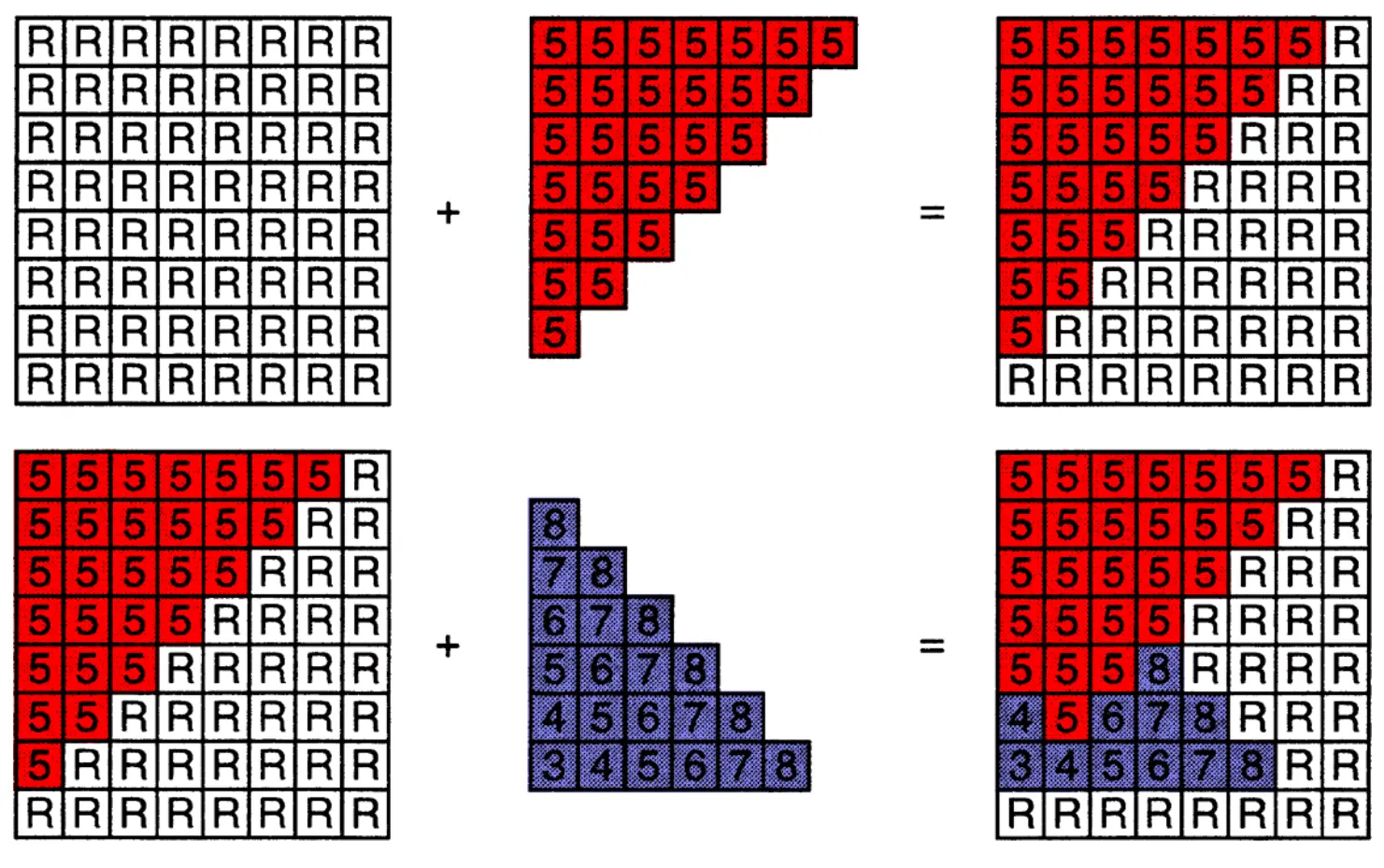
R 表示无穷大

复杂度

O(n) ：遍历 n 个三角形（每个三角形假设是常数覆盖）

不需要考虑三角形绘制顺序，可以用 GPUs 实现

Shading

对不同物体应用不同材质的过程

Blinn-Phong Reflectance Model

基本概念

Specular highlights：高光

Diffuse reflection：漫反射

Ambient lighting：环境光

局部 Shading

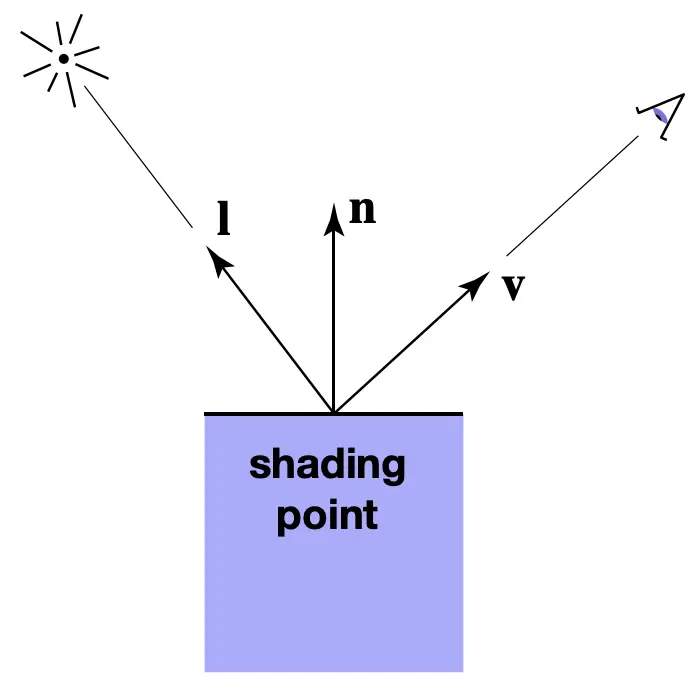
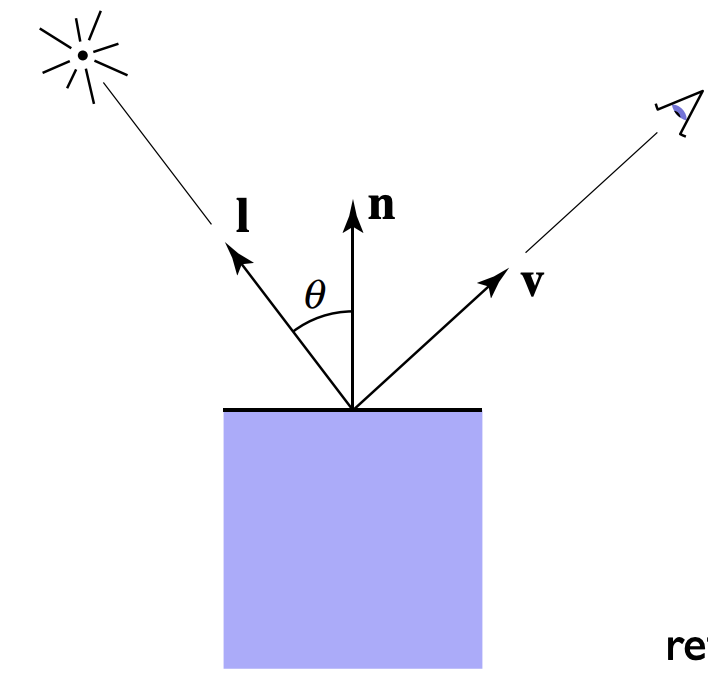
在特定的 shading point，计算光反射到 camera

• 法线，\vec{n}

• 观测方向，\vec{v}

• 光照方向，\vec{l}

• 表面参数，（color, shininess, ...）

都是单位向量

shading 不等于 shadow，shading 不会生成阴影

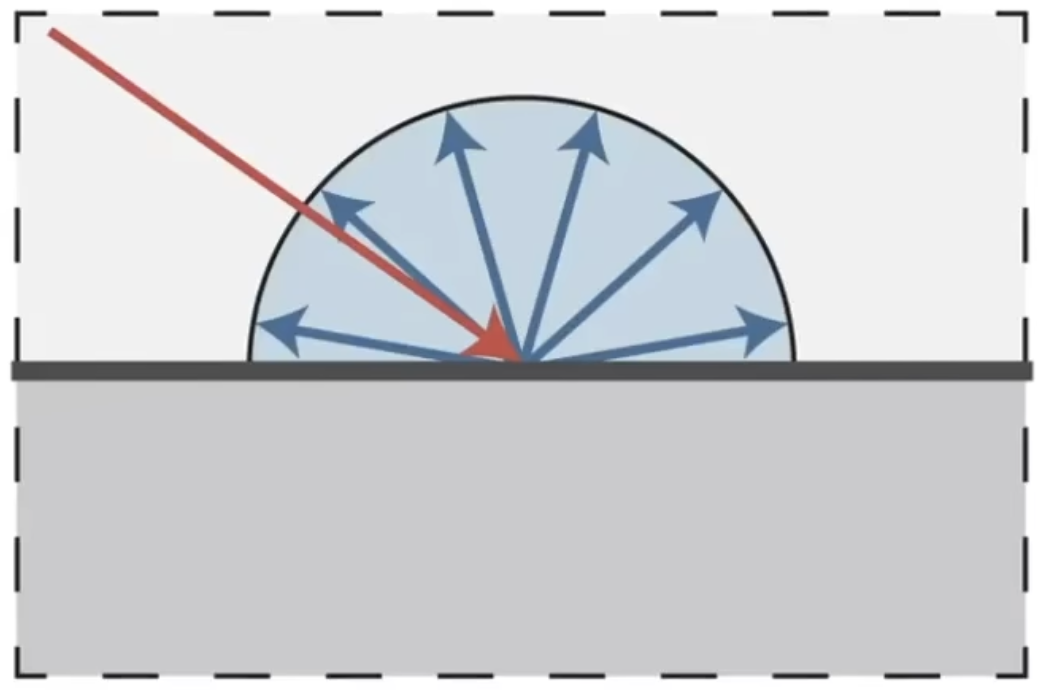
漫发射

光在各个方向均匀地散射，从任意观测方向看表面颜色是相同的

Lambert's cosine law

单位面积有多少光被接收？

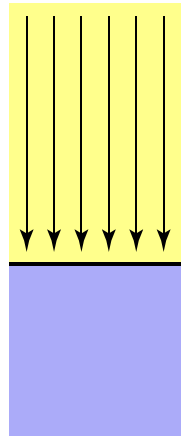
立方体的表面接收一定量的光

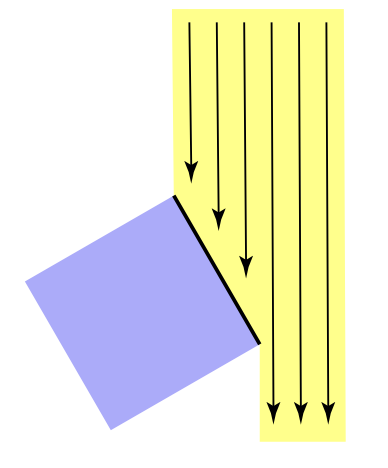
60^o旋转立方体，顶面拦截一半的光

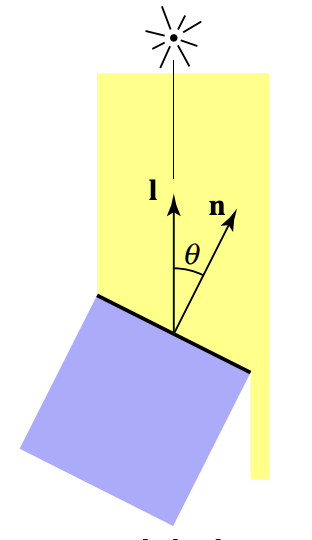
通常情况下，单位面积的光与cos\theta = \vec{l} \cdot \vec{n}成正比

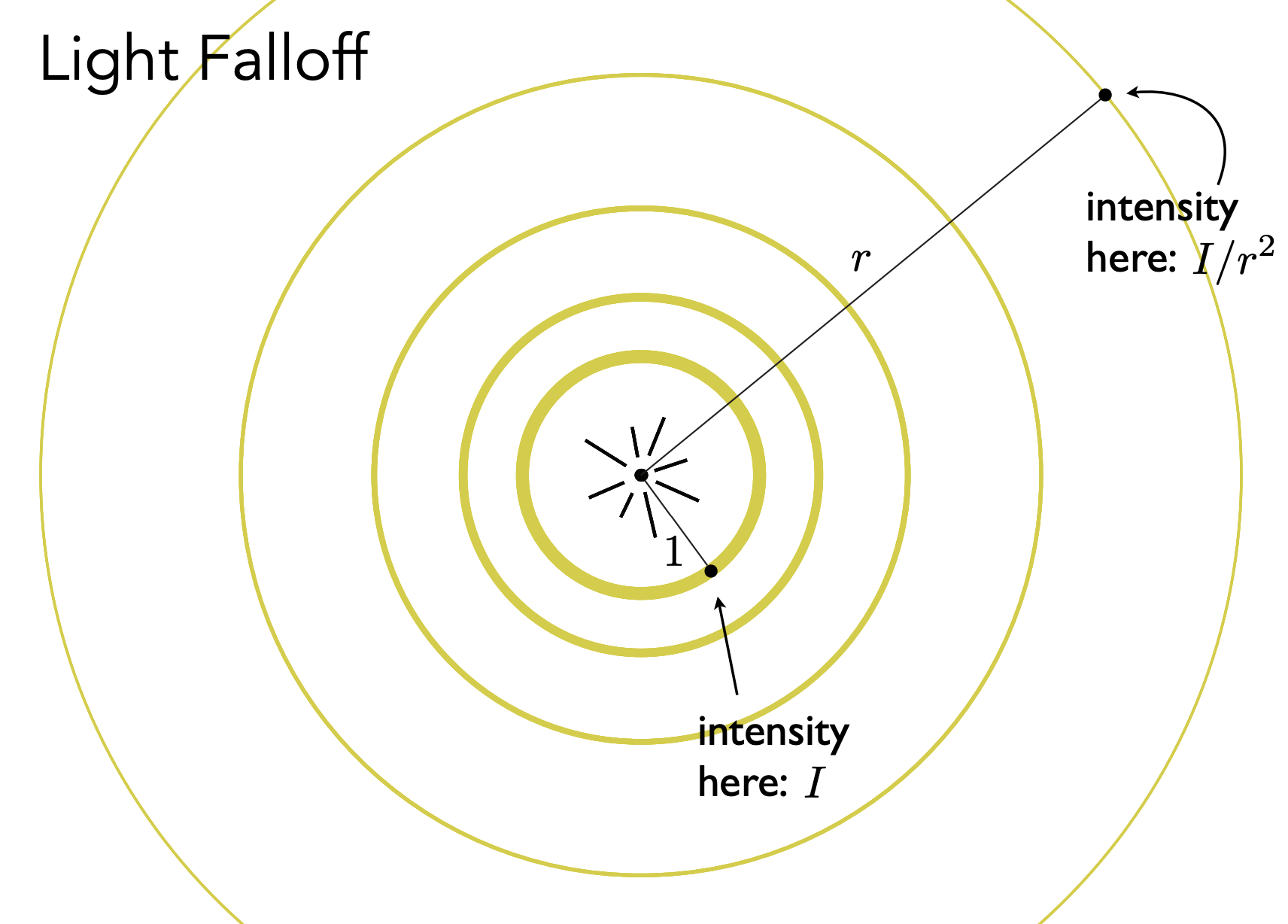
Light Falloff

Lambertian(Diffuse) Shading

Shading 独立于观察方向

L_d：漫发射光

k_d：漫反射系数(color)，表示反射率，即有多少光会被反射

r：光源到 shading point 的距离

max(0, \vec{n}\cdot\vec{l})：有多少光可以到达 shading point