插值

为什需要插值？

明确每个顶点的值；
在三角形内获得平滑的过渡。

哪些顶点属性需要插值？

纹理坐标(Texture coordinates)，colors，法线向量(normal vectors)，...

如何插值？

重心坐标(Barycentric Coordinates)

重心坐标

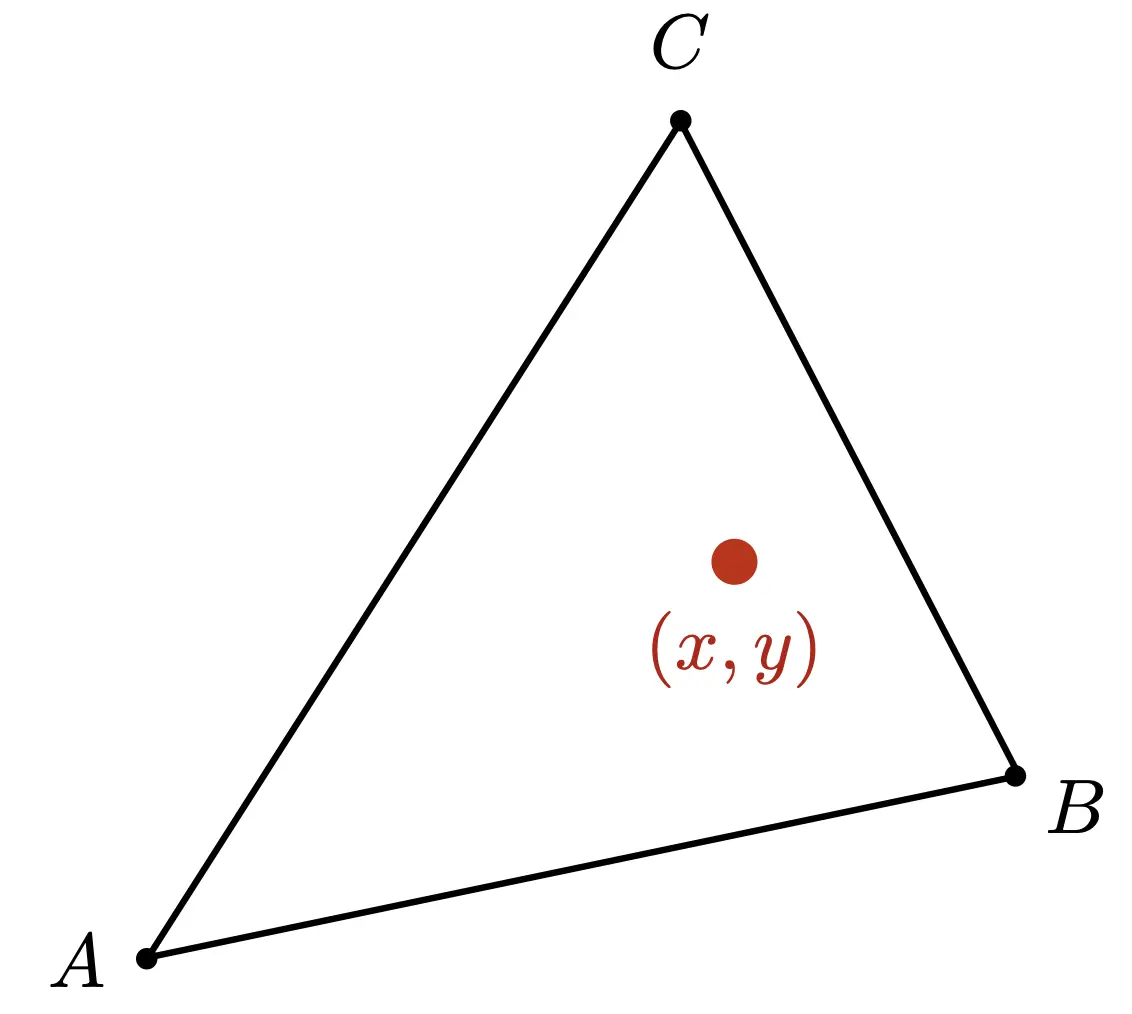
重心坐标是定义在三角形上的，换了一个三角形就是另一套重心坐标，(\alpha, \beta, \gamma)。

(x, y) = \alpha A + \beta B + \gamma C

\alpha + \beta + \gamma = 1

如果\alpha, \beta, \gamma都是非负的，表示在三角形内部，否则，在三角形这个平面内。

举例：A 点的重心坐标

(\alpha, \beta, \gamma) = (1, 0, 0) \\ (x,y) = \alpha A + \beta B + \gamma C = A

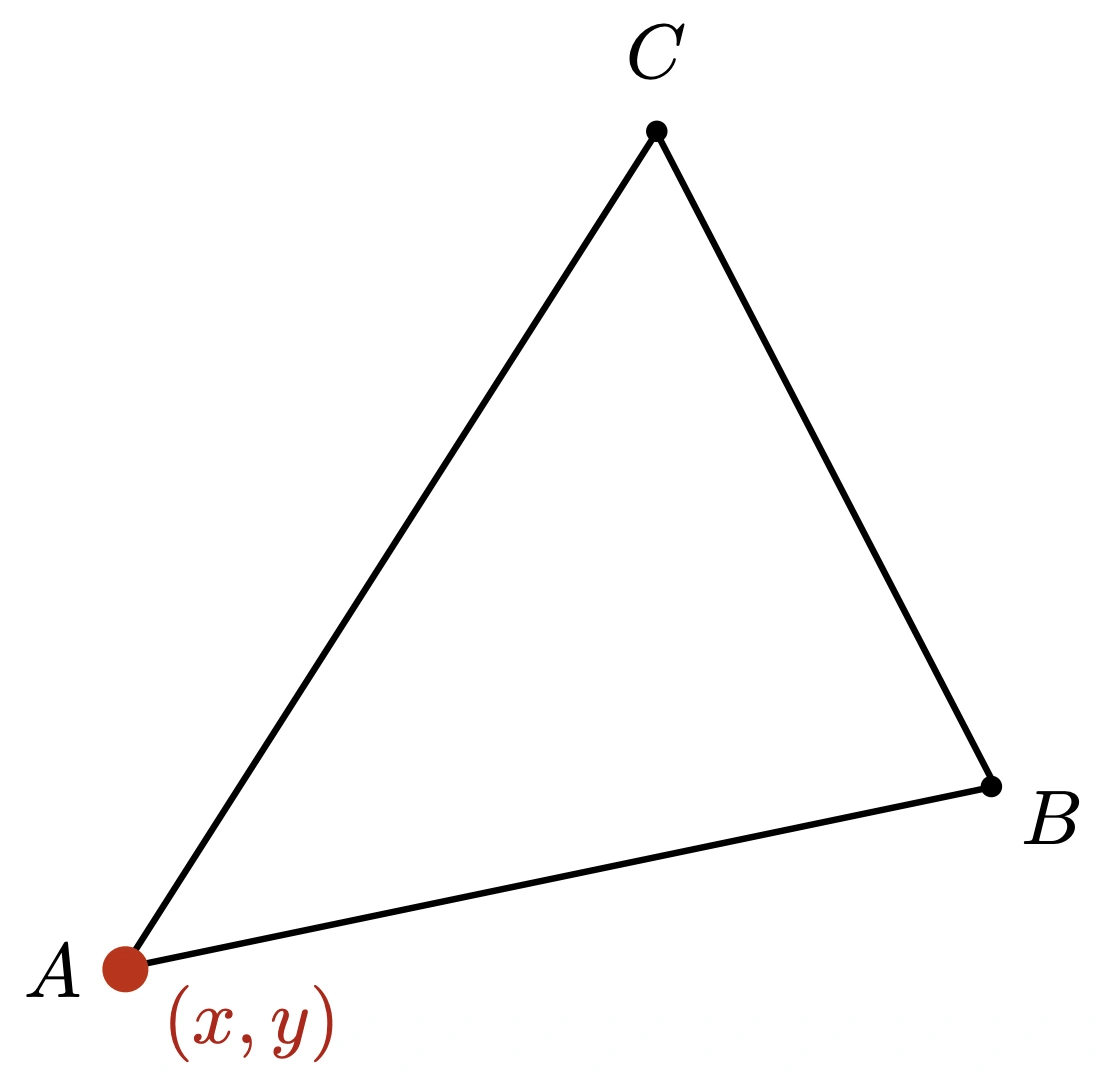
任意一点重心坐标

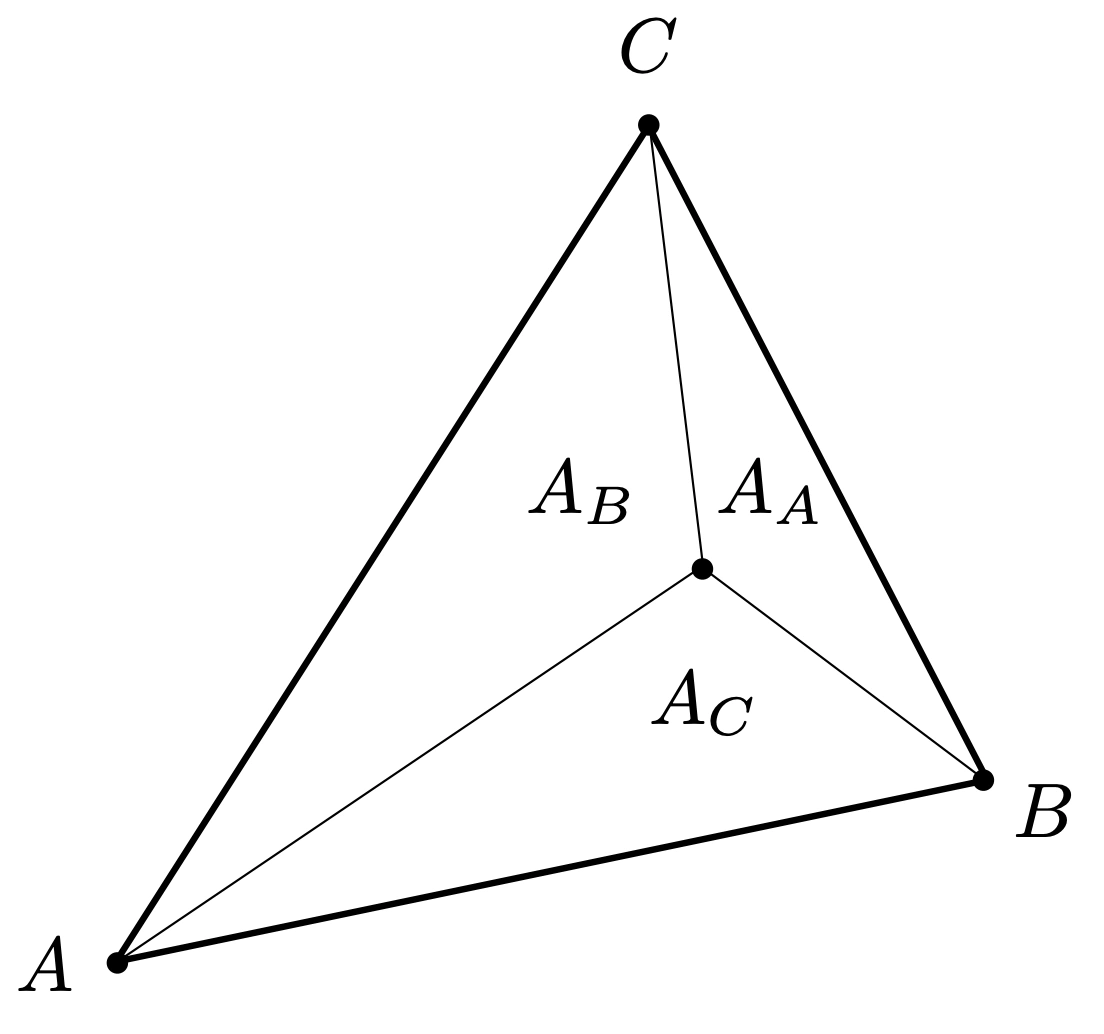
A_A表示 A 点对应三角形的面积，其余同理

\alpha = \frac{A_A}{A_A+A_B+A_C} \\ \beta = \frac{A_B}{A_A+A_B+A_C} \\ \gamma = \frac{A_C}{A_A+A_B+A_C}

三角形的重心

(\alpha, \beta, \gamma) = (\frac{1}{3}, \frac{1}{3}, \frac{1}{3}) \\ (x, y) = \frac{1}{3}A + \frac{1}{3}B + \frac{1}{3}C

计算公式

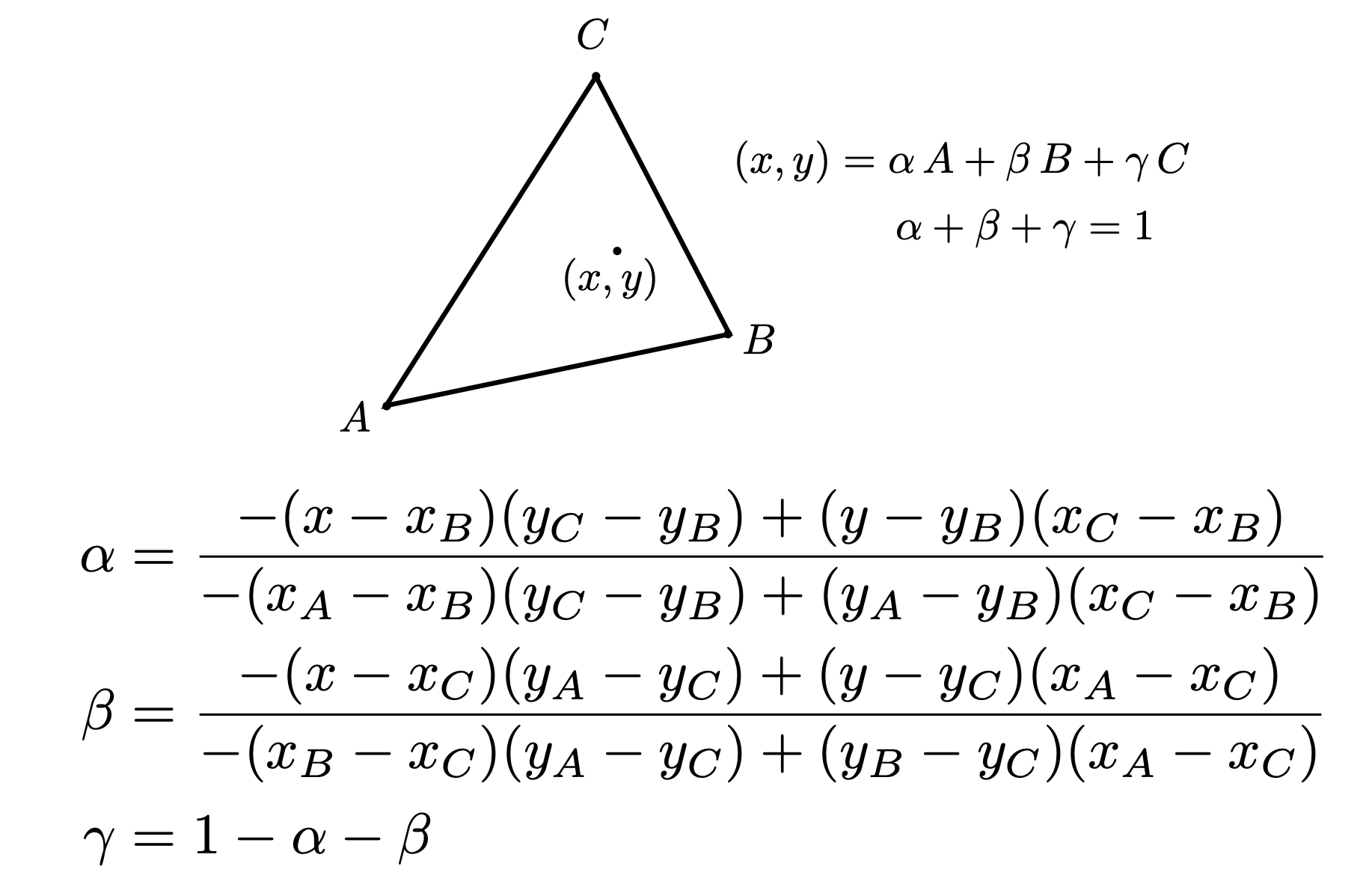
使用重心坐标

V = \alpha V_A + \beta V_B + \gamma V_C

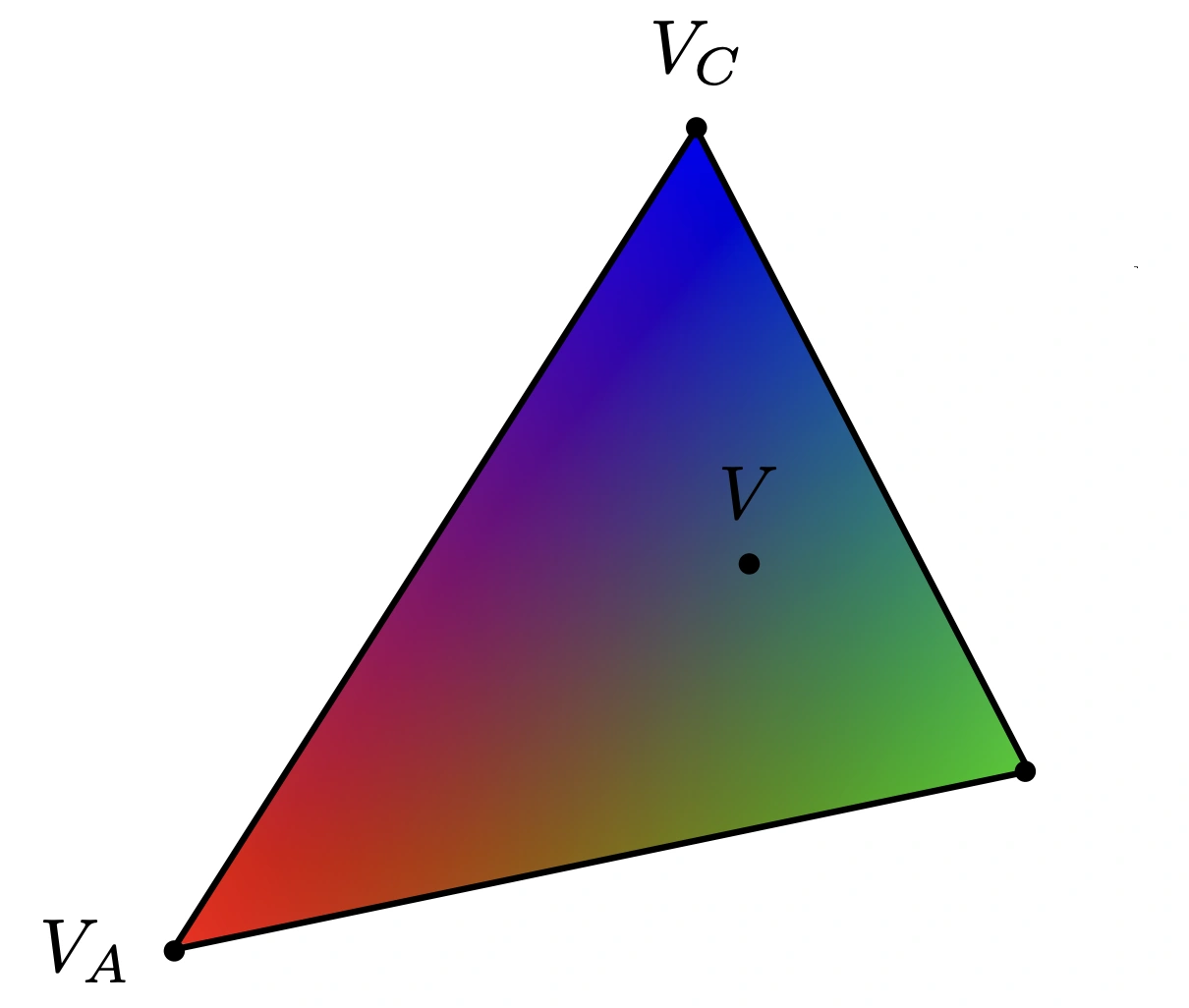
V_A, V_B, V_C可以是 positions, texture coordinates, color, normal, depth, material attributes...

注意：在投影变换后，重心坐标会发生变换，因此三维空间的顶点属性需要使用三维坐标进行计算，即二维屏幕的顶点需要逆变换回三维空间下进行计算。

应用纹理

简单的纹理映射：漫反射

for each rasterized screen sample (x, y): // 通常是像素中心
	(u, v) = evaluate texture coordinate at (x, y) // 使用重心坐标
	texcolor = texture.sample(u, v);
	set sample's color to texcolor;

texcolor：通常是漫反射率 Kd（回忆 Blinn-Phong 反射模型）

纹理放大（简单的情况）

纹理分辨率不足

A pixel on a texture -- a texel（纹理元素、纹素）

Nearest：像素映射的纹理坐标，四舍五入，因此，多个像素会映射到同一个 texel

双线性插值

Bilinear Interpolation

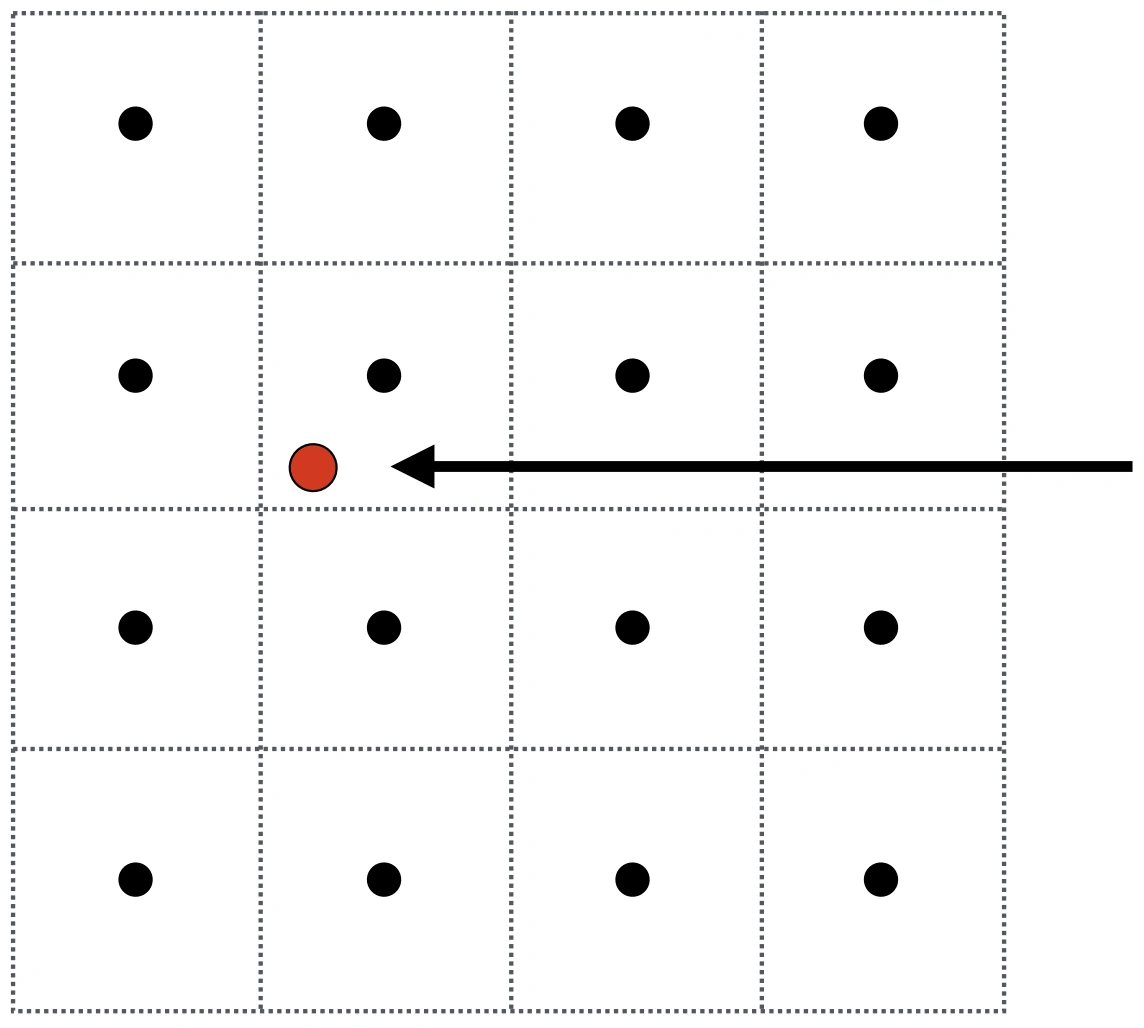
红色点代表像素点，黑色点代表纹理采样位置

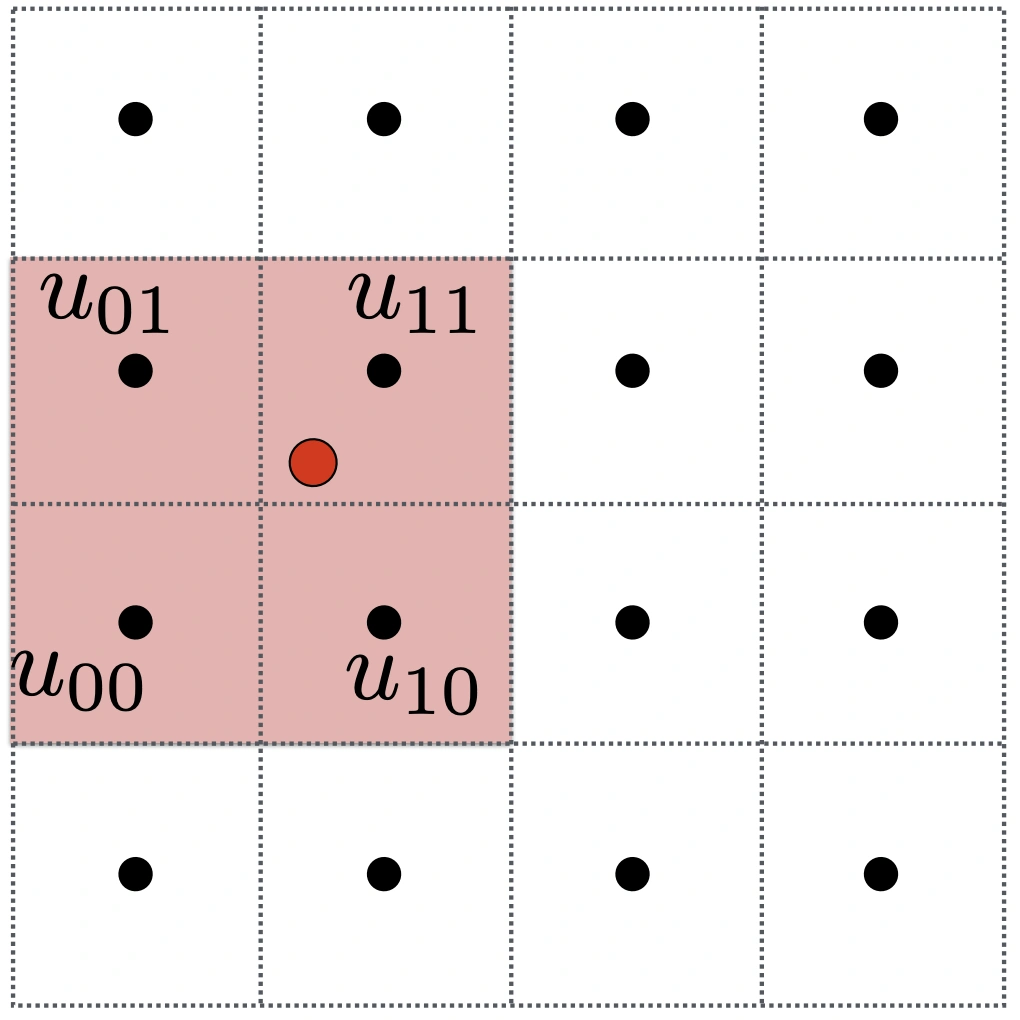
取临近的 4 个采样位置，texture values 被标记

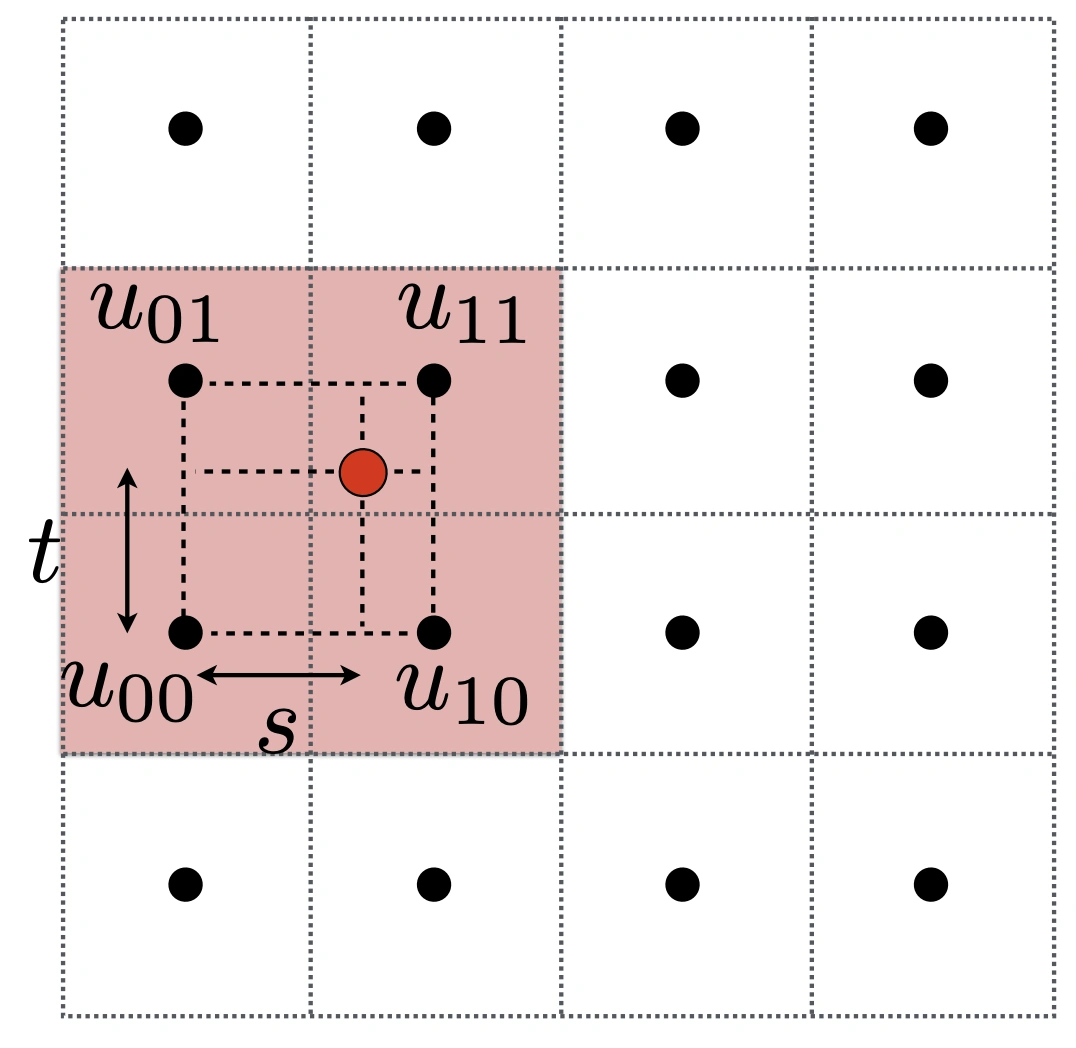
s 和 t 在 0～1 之间

线性插值（1D）

lerp(x, v_0, v_1) = v_0 + x(v_1 - v_0)

u_0 = lerp(s, u_{00}, u_{10}) \\ u_1 = lerp(s, u_{01}, u_{11})

f(x,y)=lerp(t,u_0,u_1)

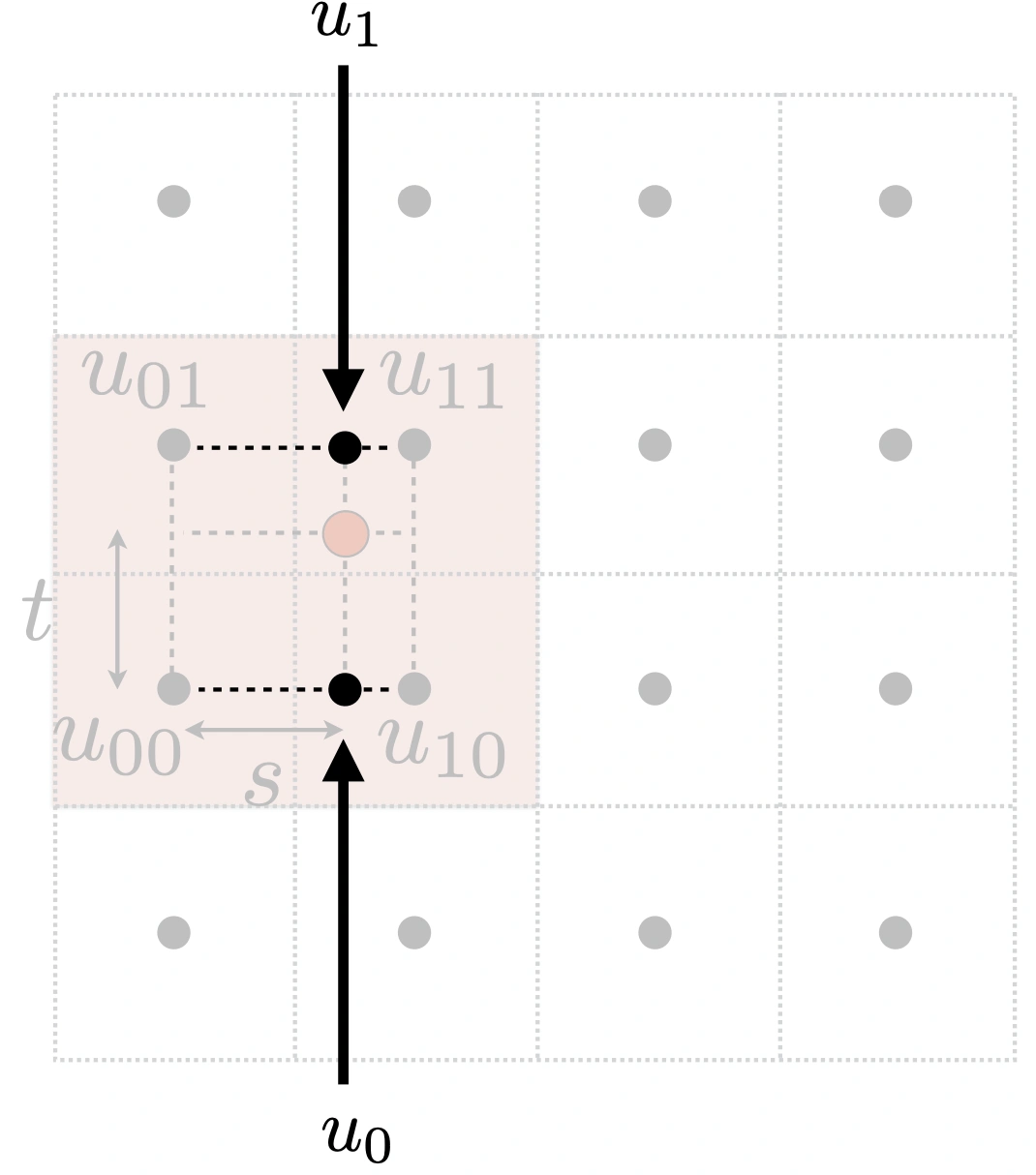
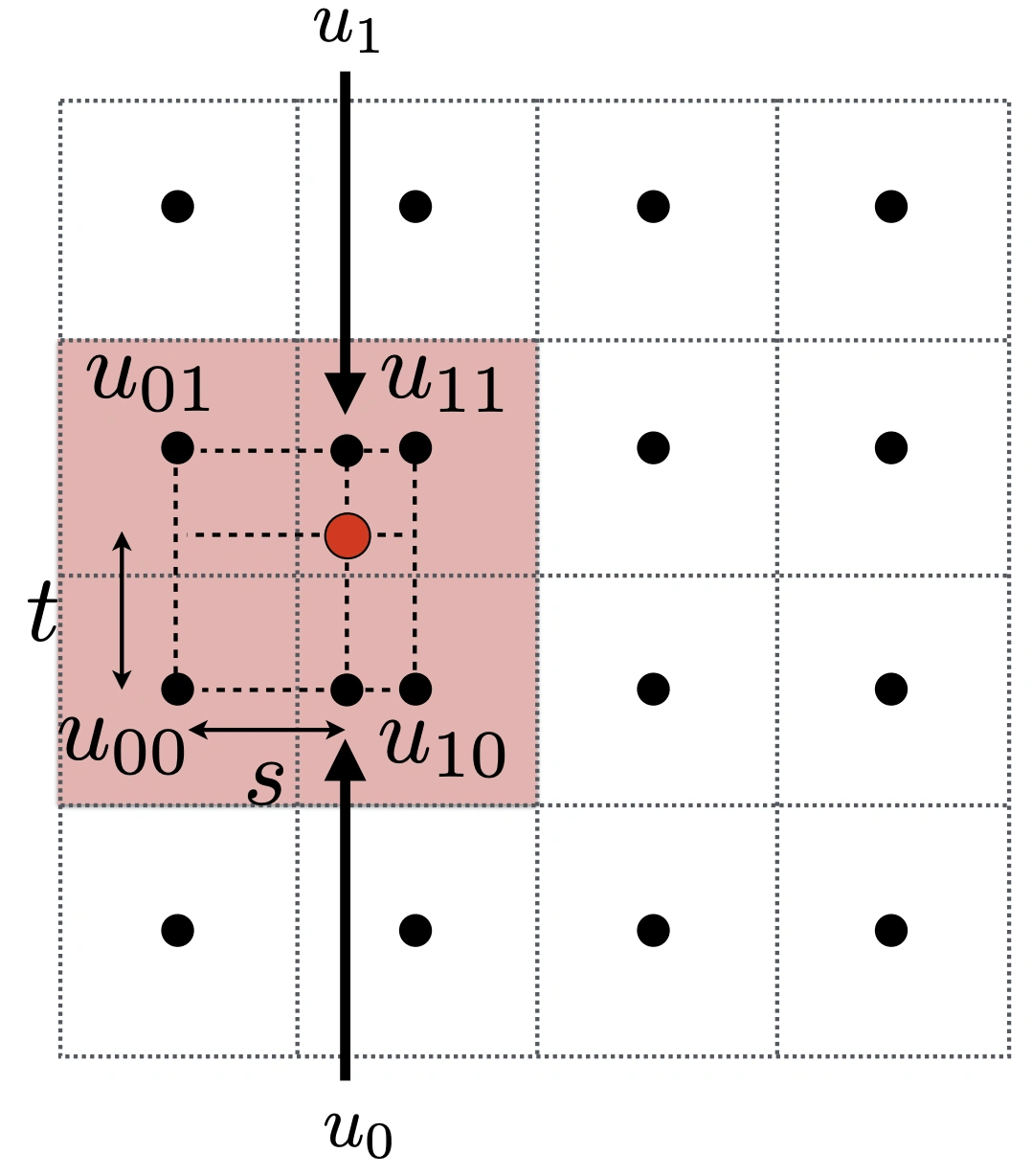
结果

在合理的消耗下，可以取得不错的效果。

纹理放大（困难的情况）

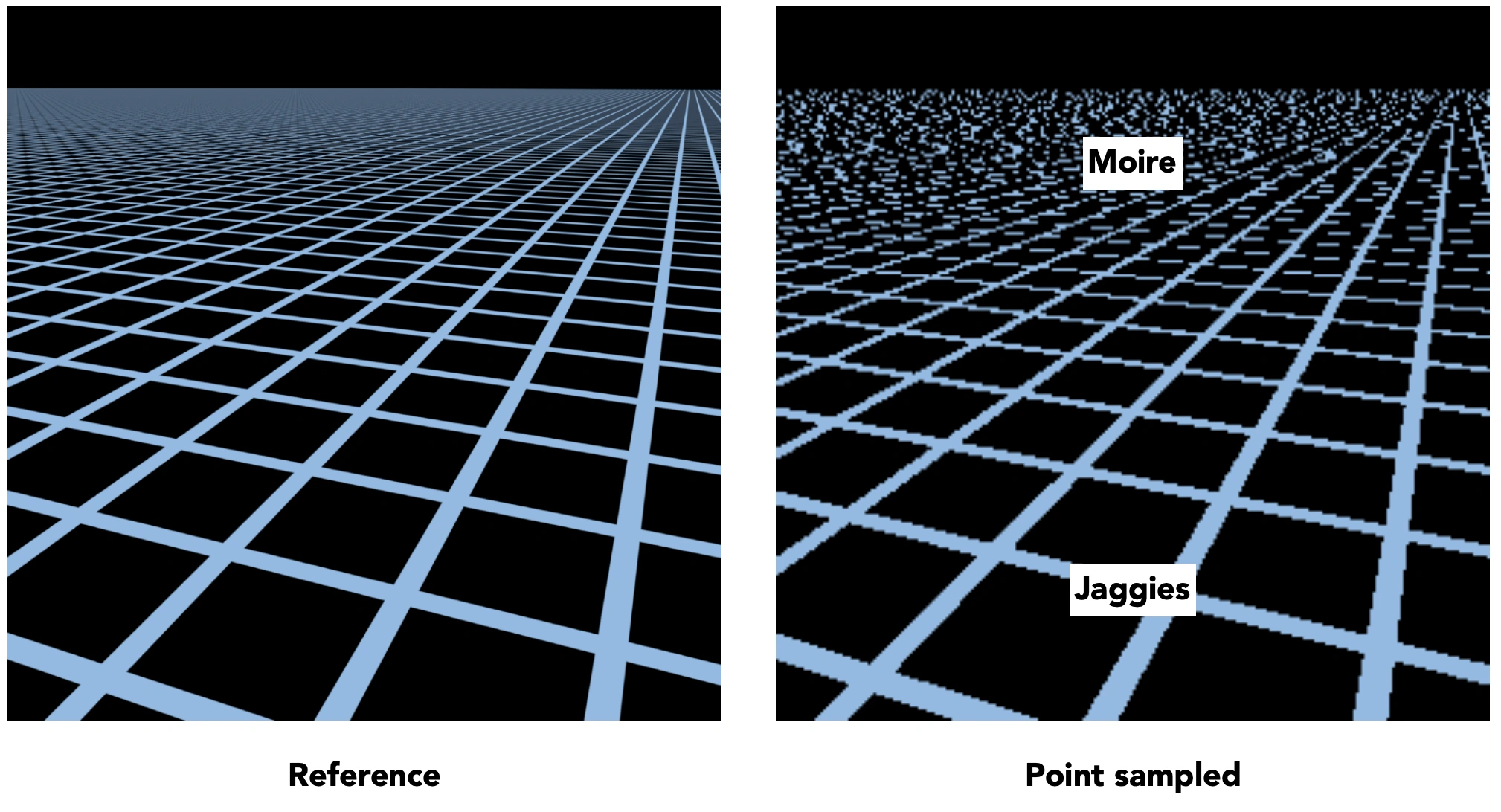
产生的原因

近处像素覆盖的纹理区域较小，远处像素覆盖的纹理区域较大，因此远处用像素中心采样的结果不正确

每个像素用 512 个采样点来对应纹理坐标

走样产生的原因：信号速度变化过快，采样速度跟不上。

当纹理特别大的时候，一个像素内可能包含很大的纹理，这块纹理在不停地变化，即在像素内纹理变化频率很高，但只用了一个采样点。

supersampling 质量很高，但是消耗太大

如何解决这个问题？

得到一个范围内的平均值

点查询和范围查询

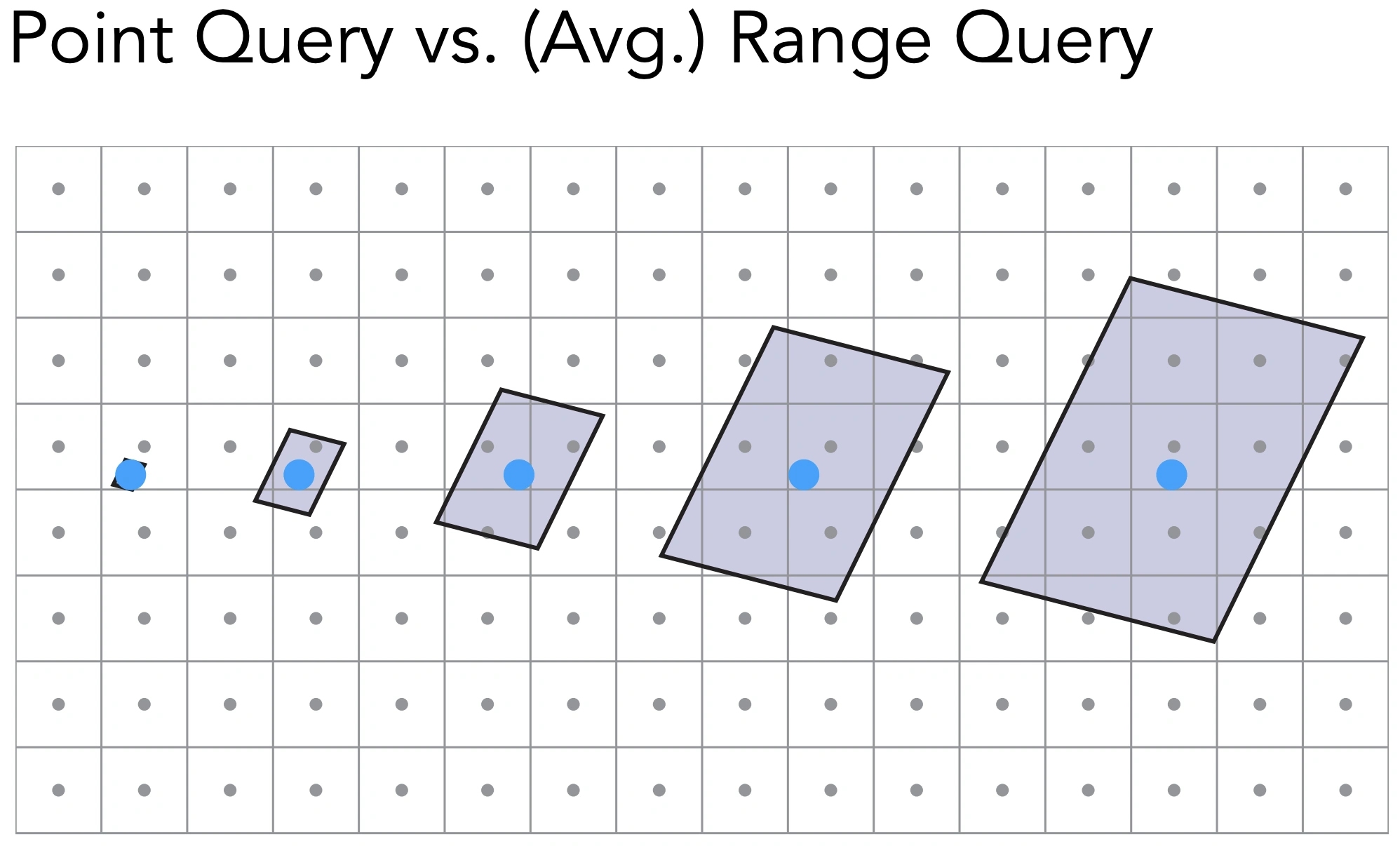
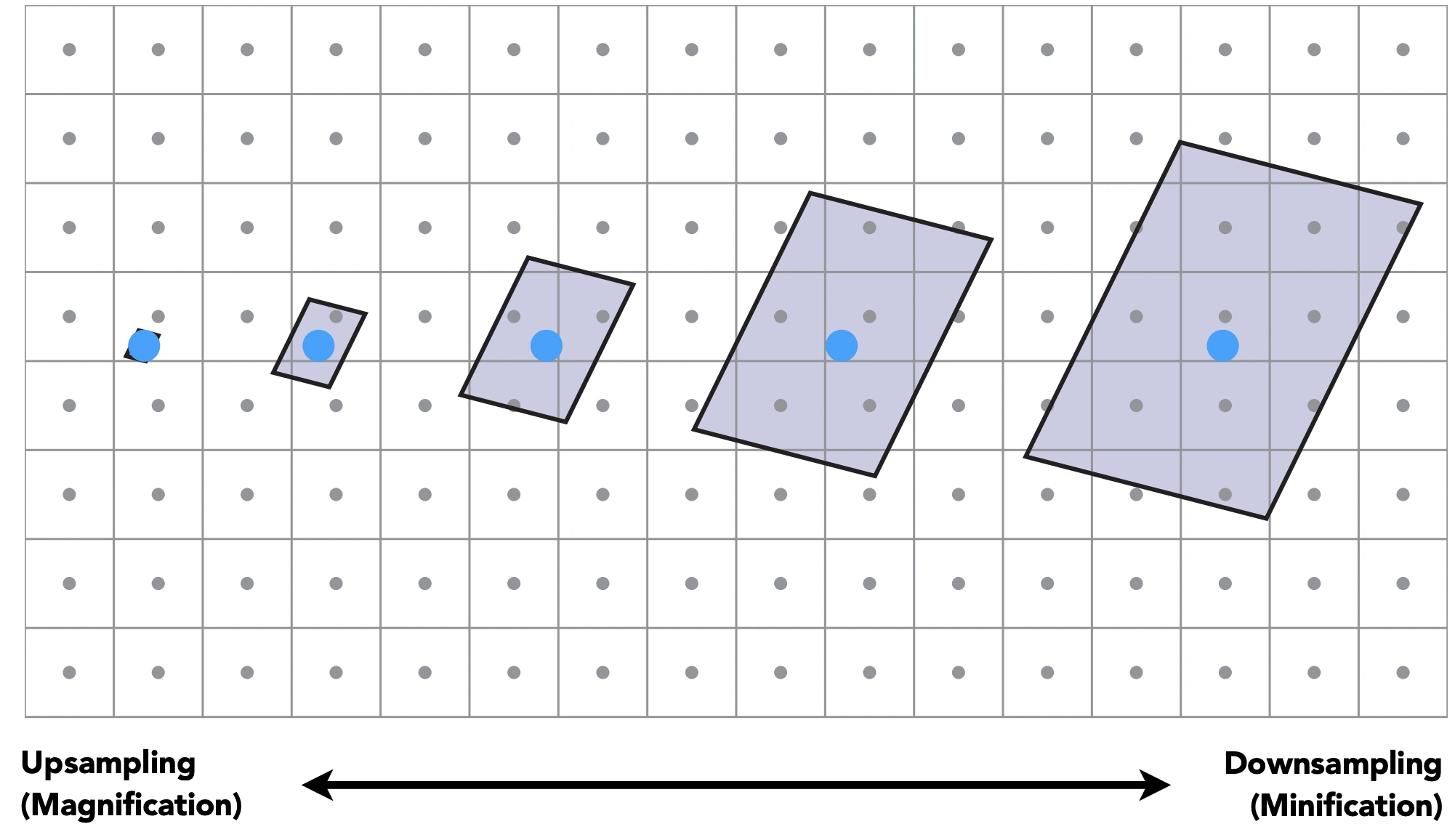
点查询：给一个点，求值，例如双线性插值

范围查询：例如给定一个区域，可以立刻得到平均值

Mipmap

允许范围查询（快，近似，方形）

从一张图生成一系列图，像素逐渐递减

额外存储原来大小的 1/3

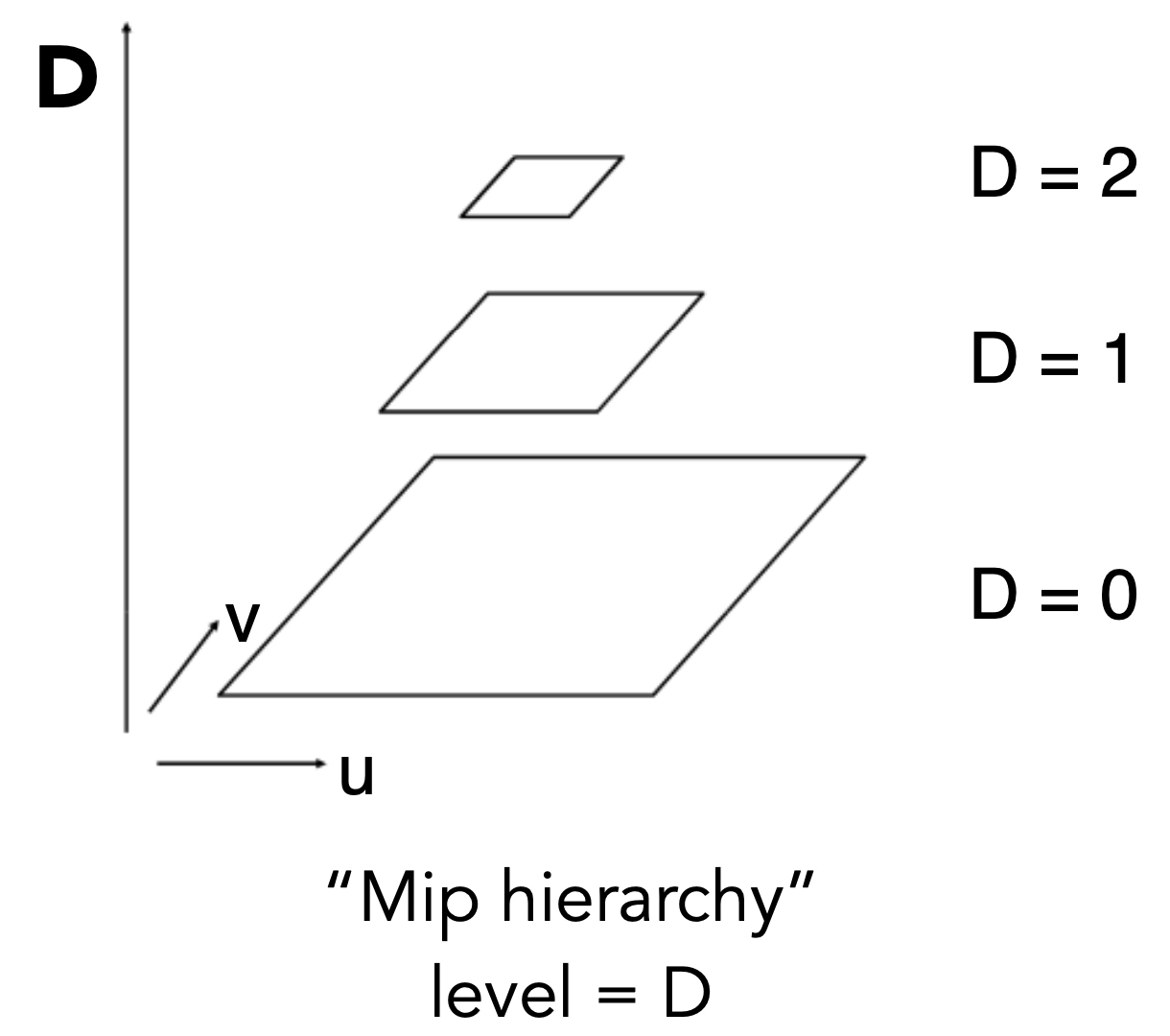
计算 Mipmap Level D

使用屏幕采样点及相邻的采样点评估纹理图所占区域

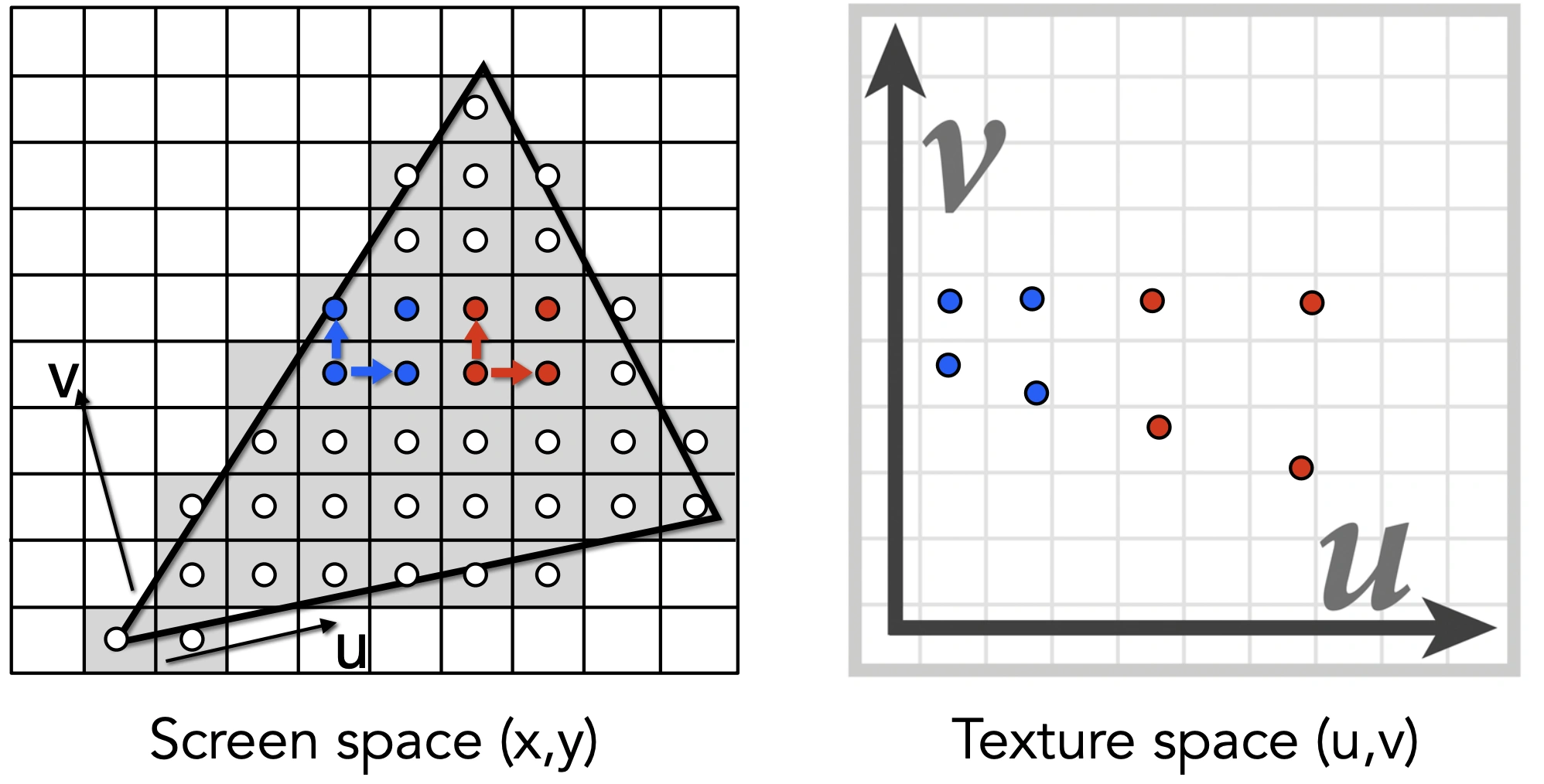
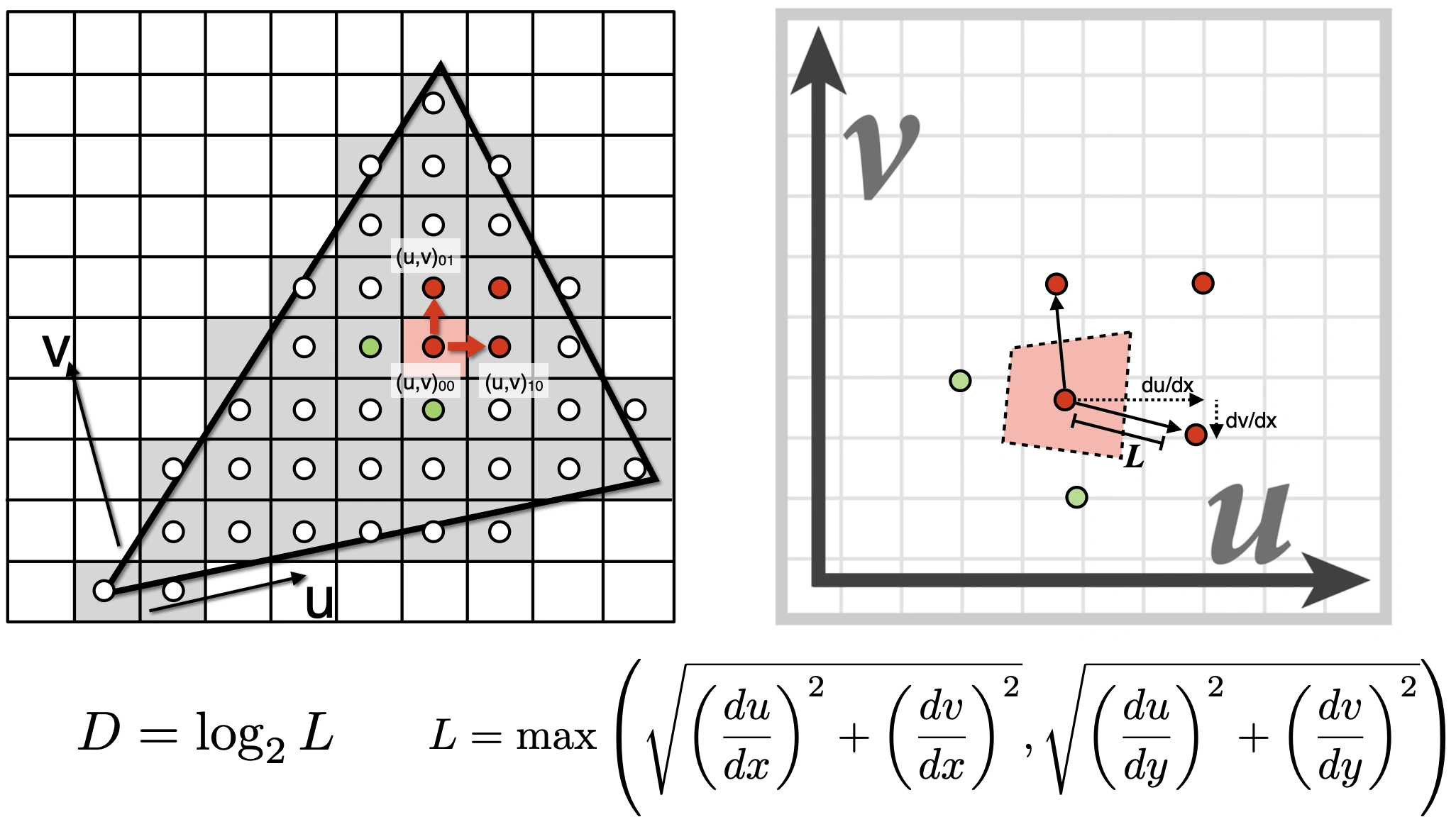
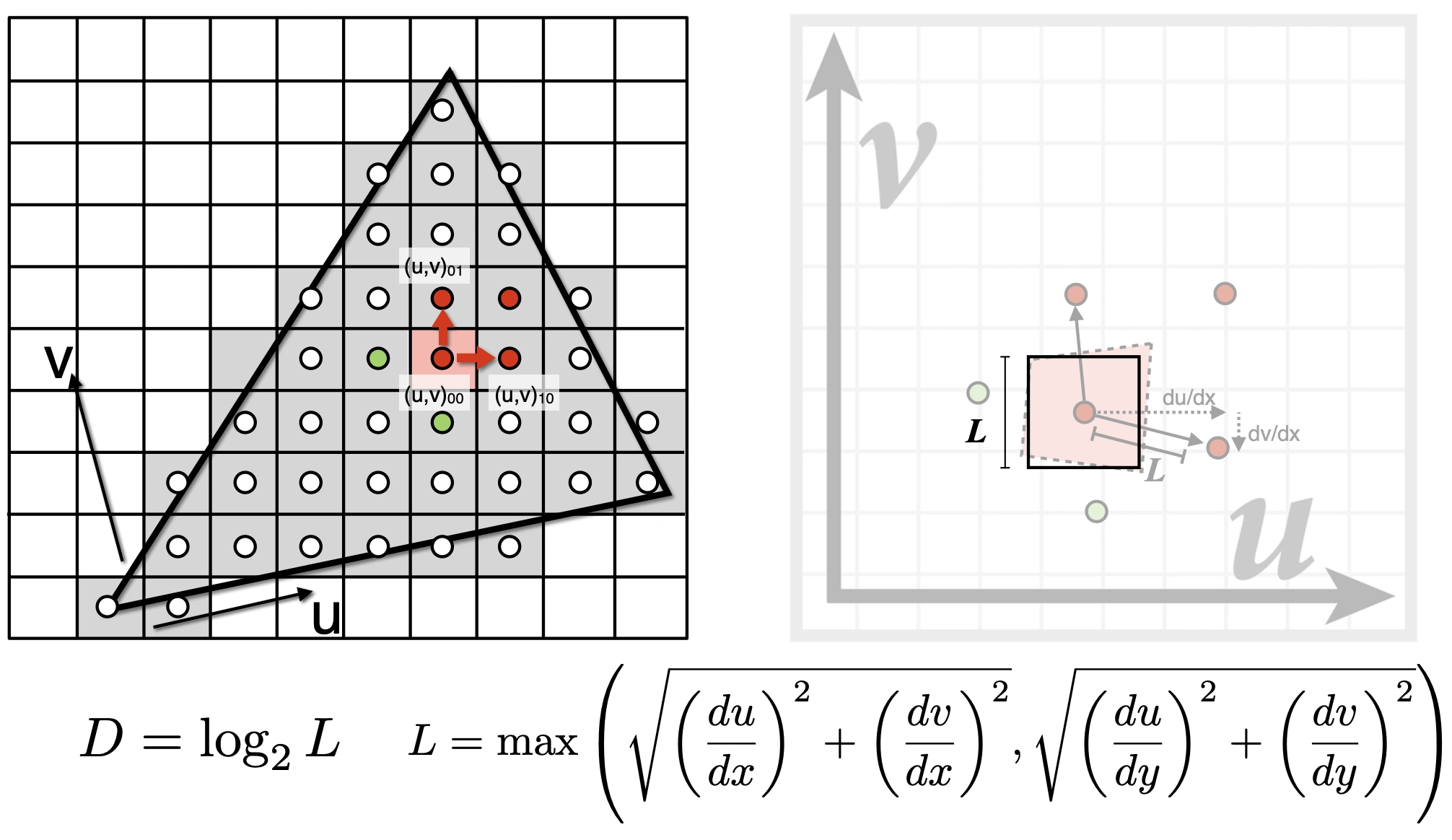
在 D 层，L 会变成一个像素

Mipmap Level 可视化

离散的若干层，变化不连续，可能存在缝隙，因此希望可以查询到类似 1.8 层，解决方法：插值

Trilinear Interpolation

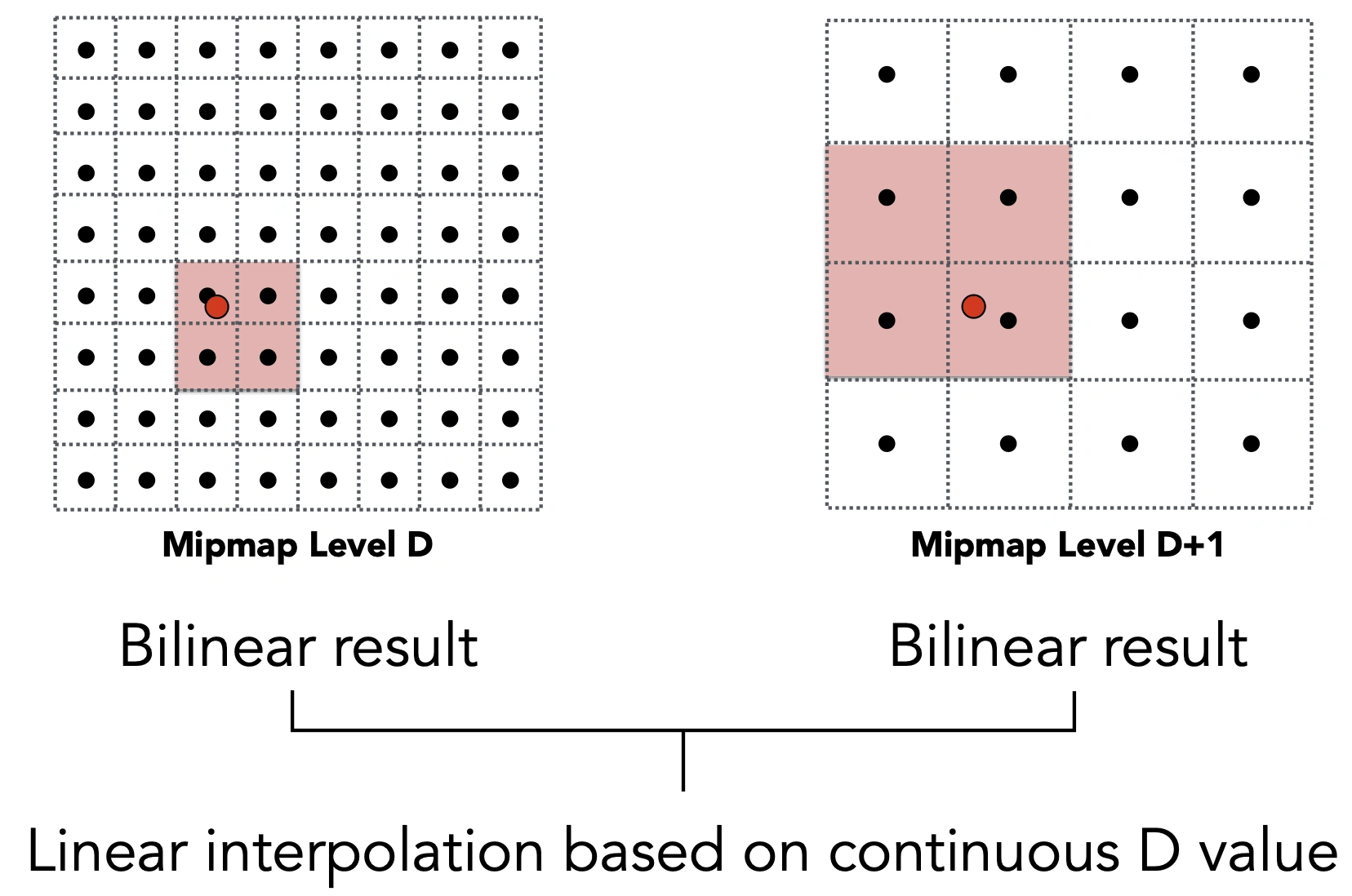
修正之后可视化

不同区域之间存在过渡

过渡模糊

只能计算方块区域
插值本身是近似

各向异性过滤（Anisotropic filtering）

mipmap 相当于对角线，在此基础上增加

水平方向，高度不变，宽度减半；垂直方向，宽度不变，高度减半。即不均匀的水平和竖直方向上的压缩

相当于多出一个矩形区域，不用限制在正方形区域中

Ripmaps

原因

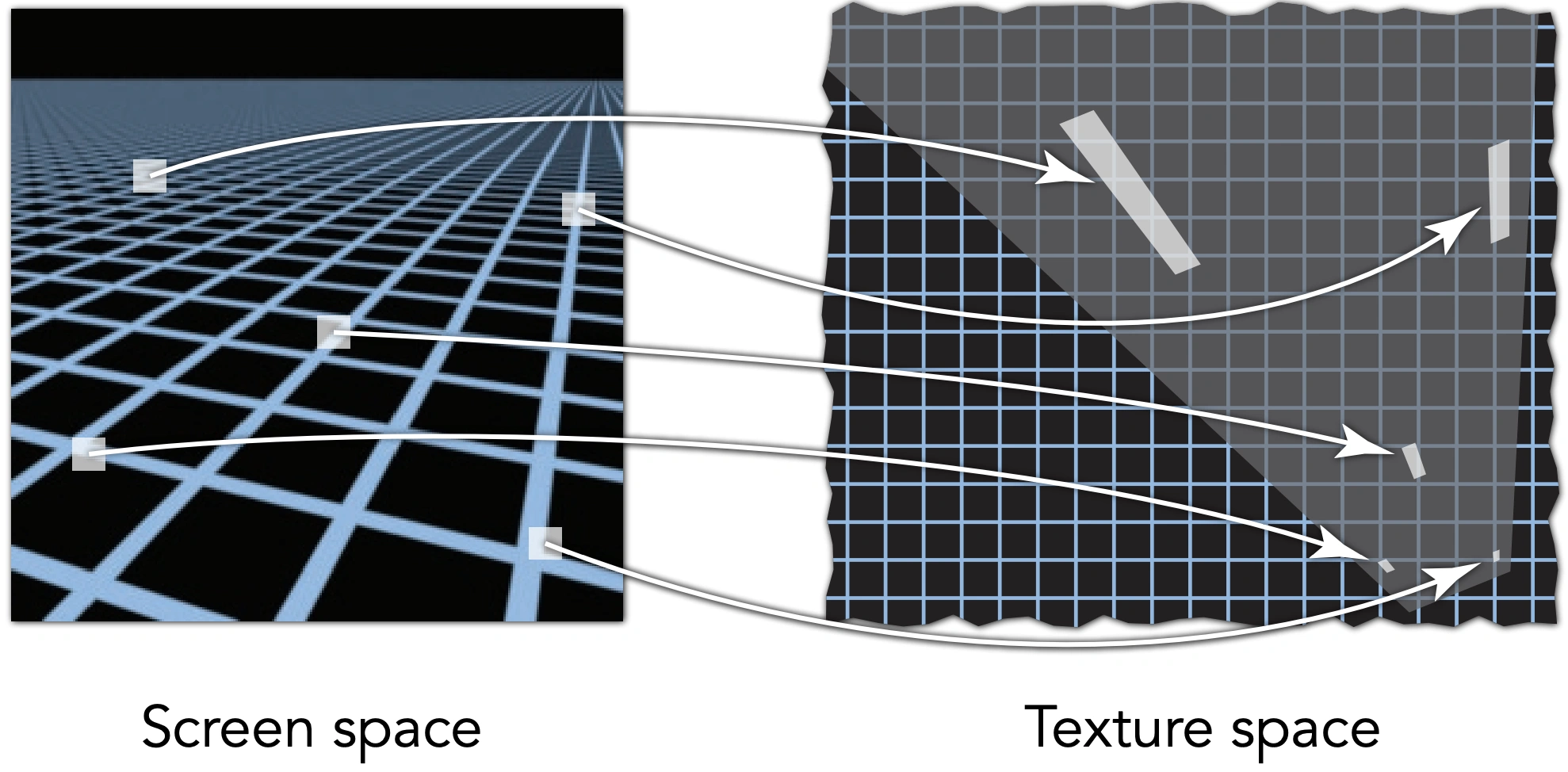
映射到纹理区域，不一定是规律的形状。各向异性过滤仍然没有解决问题。

插值