结论
对于带有不均匀缩放的变换矩阵,直接与其相乘会得到错误结果。
示例
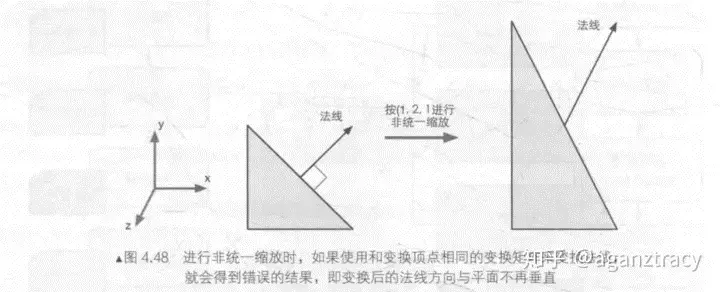
按照普通矢量在 y 轴方向放大 2 倍的规则,“y 分量乘以 2”对法线也进行放大。
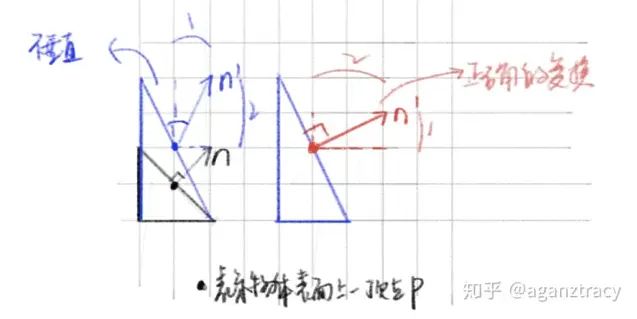
为了保证法线垂直于平面,正确的做法是,不仅不能让法线放大,反而还要在那个轴向上缩小,也就是普通向量“y 分量乘以 2”,法线向量反而是"y 分量除以 2",这就是法线具有逆缩放的特性。
总结
法向量的变换矩阵中缩放矩阵应该是原来顶点变换缩放矩阵的逆矩阵,而法向量的旋转矩阵应保持原本的旋转。
而 MODELVIEW 矩阵已经是旋转和缩放乘法在一起的组合体,很难重新提取出缩放和旋转两个部分并对缩放单独求逆,平移部分由于只涉及第四行的三个分量,而法线作为相对矢量只需要考虑矩阵 3x3 部分的分量,因此可以不考虑平移。
已知对于普通相对矢量的变换矩阵M = SR,我们想要获取的是针对法线矢量的变换矩阵M^’ = S^{-1}R,如何获取?答案就是求原矩阵的逆转置,也就是说M’= (M^{-1})^T。
(M^{-1})^T = ((SR)^{-1})^T = (R^{-1}S^{-1})^T = (S^{-1})^{T}(R^{-1})^T
旋转矩阵求转置就是求逆R^{T} = R^{-1},缩放矩阵的转置后不变S^T = S。
(S^{-1})^T(R^{-1})^T = (S^T)^{-1}(R^T)^{-1} = S^{-1}(R^{-1})^{-1} = S^{-1}R = M^’
最后对法线进行重新归一化才能用于光照计算。
