参考赵新政——从 0 开始实现 OpenGL
如何在屏幕上绘制直线
给到两个点p_1(x_1, y_1),p_2(x_2, y_2),请在屏幕像素空间绘制一条直线。
条件:
x_1 < x_2,斜率0 < k < 1
最简单的方案
直线方程:
y = kx + b\\ k=(y_2-y_1)/(x_2-x_1)
算法:
x = x1;
while(x < x2) {
y = (int)(kx + b);
drawPoint(x, y);
x++;
}缺点:
有一次 k*x 这样的浮点数乘法运算以及一次 +b 这样的浮点数加法,效率比较低。
Brensenham 直线绘制算法
只使用整数型数据进行运算与决策,省略了浮点数运算,从而提高了绘制效率。
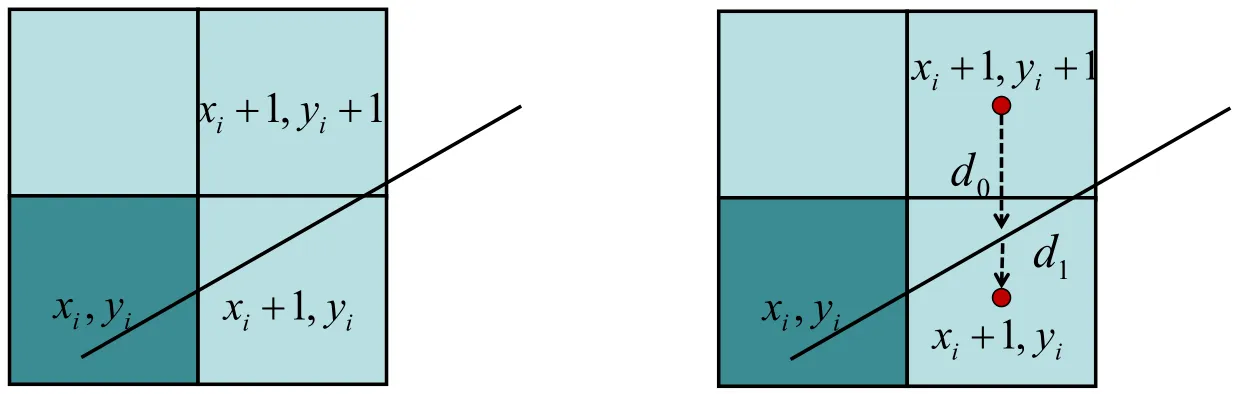
假设当前直线已经通过点x_i,y_i,当 x 方向向前步进 +1 的时候,如何能够决定 y 的选项呢?
d_0 = y_i + 1 - k(x_i + 1) - b \\ d_1 = k(x_i + 1) + b - y_i
d_1 - d_0 = k(x_i+1)+b-y_i-y_i-1+k(x_i+1)+b \\ = 2k(x_i+1)-2y_i-1+2b
由已知条件:
k = (y_2-y_1)/(x_2-x_1) \\ \Delta x=(x_2-x_1) > 0
等式两边同乘以 \Delta x 表达式的正负号不会发生变化
p_i = \Delta x(d_1-d_0)=2\Delta y(x_i+1)-(2y_i+1-2b)\Delta x \\ = 2 \Delta yx_i - 2\Delta xy_i+(2\Delta y + 2b\Delta x - \Delta x)
使用p_i的正负即可判断选择哪个栅格
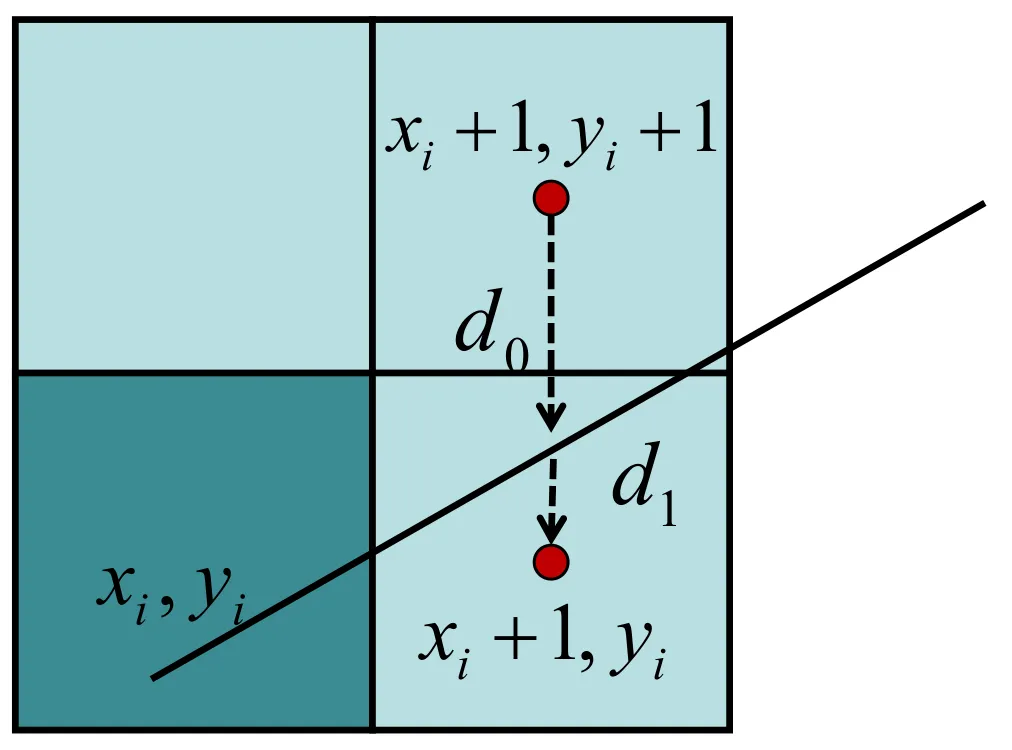
p_i > 0 \ \ d_1 > d_0 \ \ y_{i+1} = y_i + 1 \\ p_i < 0 \ \ d_1 < d_0 \ \ y_{i+1} = y_i
迭代模型
p_i = 2\Delta yx_i - 2\Delta xy_i + (2\Delta y + 2b\Delta x - \Delta x) \\ p_{i+1} = 2\Delta y(x_i + 1) - 2\Delta xy_{i+1} + (2\Delta y + 2b \Delta x - \Delta x) \\ p_{i+1} - p_i = 2\Delta y - 2\Delta x(y_{i+1} - y_i)
考察第一个 p 值,带入x_1, y_1 = kx_i + b
p_1 = 2 \Delta yx_1 - 2\Delta x(\frac{\Delta y}{\Delta x}x_1 + b) + (2\Delta y + 2b\Delta x - \Delta x) \\ p_1 = 2\Delta y - \Delta x
得到如下算法
x = x_1; y = y_1; \\ p = 2\Delta y - \Delta x \\ WHILE(x < x_2) \{ \\ drawPoint(x, y); \\ x++; \\ if(p >= 0) \{ \\ y = y + 1; \\ p = p - 2\Delta x \\ \} \\ p = p + 2 \Delta y \\ \}
注意:本方法只对满足前置条件的直线生效。
扩展更多情况
考虑只满足x_1 < x_2,y_1 < y_2,但是k > 1的情况
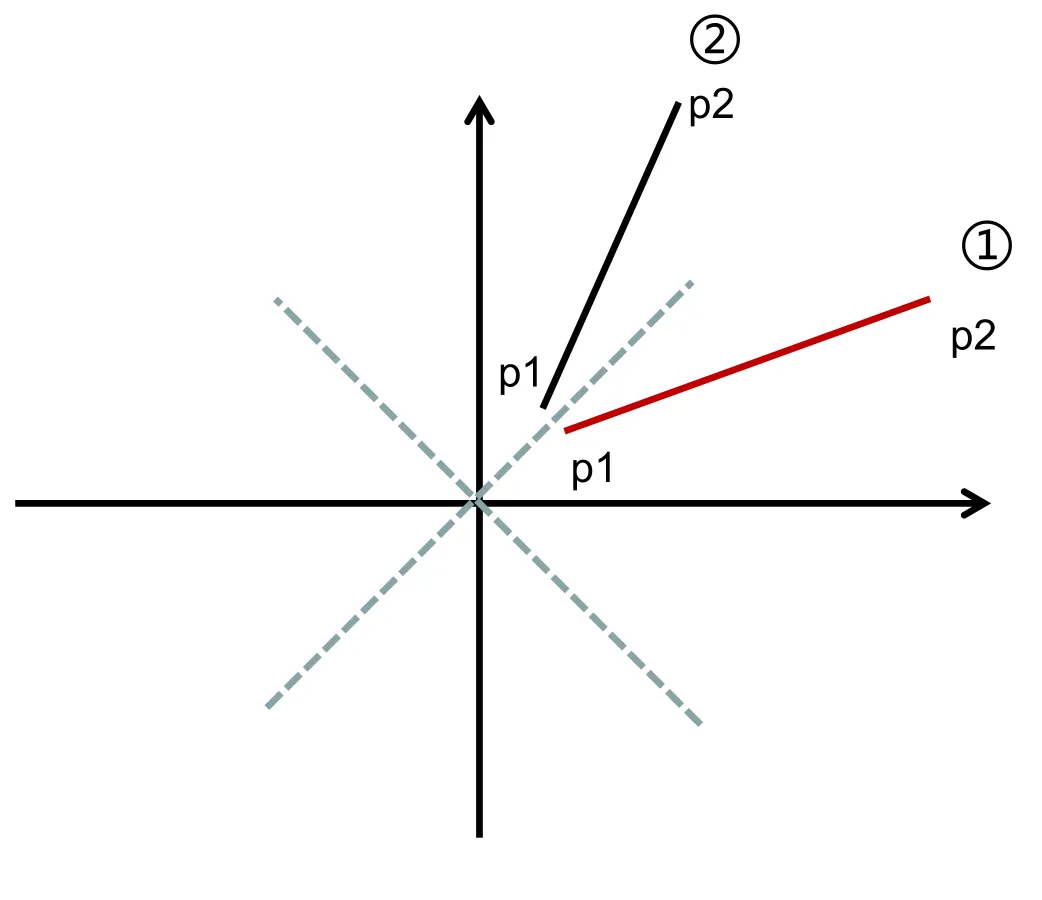
只需要把两个点的 xy 值各自互换就可以。
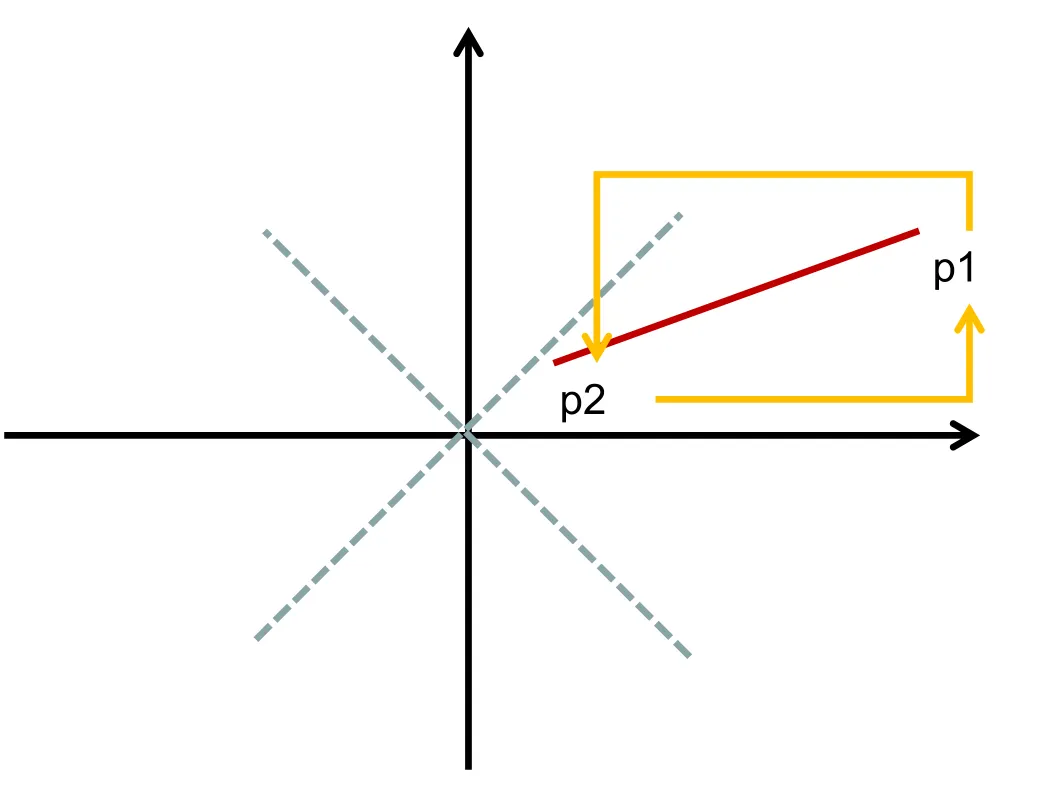
考虑x_1 < x_2,y_1 > y_2的情况
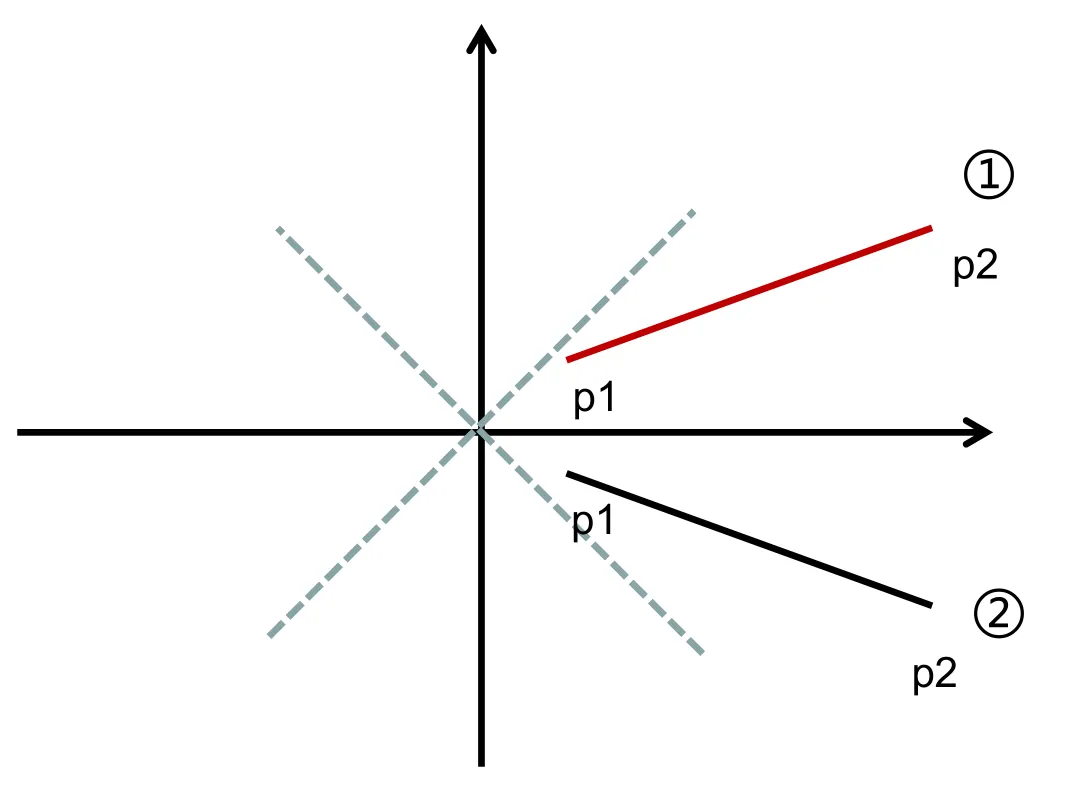
只需要把两个点的 y 值变符号即可达到第一象限。
考虑x_1 > x_2,y_1 > y_2的情况
只需要把绘制起始点与中止点互换即可。
