https://www.redblobgames.com/maps/terrain-from-noise/

前言

我网站上最受欢迎的页面之一，是关于多边形地图生成的内容。制作这类地图要花不少功夫，但我最开始并没有直接从这里入手 —— 而是从一个简单得多的方法起步，接下来就给你讲讲这个方法。用这个更简单的技术，不到 50 行代码就能生成类似这样的地图。

我不会讲解如何绘制这些地图——因为这取决于你使用的编程语言、图形库、平台等因素。我只会说明如何用高度图和生物群系地图数据填充一个数组。

噪声

生成 2D 地图的一种常用方法，是用带宽受限的梯度噪声函数（比如辛普森噪声或柏林噪声）作为基础模块。这类噪声函数的样子如下：

我们给地图上的每个位置分配一个 0.0 到 1.0 之间的数值。在这张图像中，0.0 对应黑色，1.0 对应白色。以下是用类 C 语法设置每个网格位置颜色的方法：

for(int y = 0; y < height; ++y)
{
	for(int x = 0; x < width; ++x)
	{
		double nx = x / width - 0.5, ny = y / height - 0.5;
		value[y][x] = noise(nx, ny);
	}	
}

这个循环在 JavaScript、Python、Haxe、C++、C#、Java 以及其他大多数主流编程语言中的逻辑都是一样的，所以我会用类 C 语法来展示它，你可以根据自己使用的语言进行转换。在教程的剩余部分，我会讲解：随着我们添加更多功能，循环体（也就是value[y][x] =...这行代码）会如何变化。最后，我还会给出一个完整的示例。

具体取决于你使用的库，你可能需要对获取到的数值进行偏移或乘法运算，使其适配 0.0 到 1.0 的范围。有些库直接返回 0.0 到 1.0 的数值；有些返回 -1.0 到 +1.0 的数值；还有些返回其他范围（比如 -0.7 到 +0.7）。部分库甚至不会说明返回值范围，这种情况下你可能需要查看实际返回值，才能确定其数值范围。

海拔

噪声本身只是一堆数字，我们需要为它赋予实际意义。首先能想到的，就是让噪声对应海拔（也称为 “高度图”）。我们用之前得到的噪声，把它作为海拔来绘制，效果如下:

代码几乎是一样的，唯一的区别在于内层循环的内容，现在它是这样的:

elevation[y][x] = noise(nx, ny);

对，就是这样。地图数据本身是完全一样的，只不过现在我把它叫做 “海拔（elevation）”，而不是之前的 “数值（value）”。

生成的地形有很多山丘，但除此之外就没别的东西了。问题出在哪儿呢？

频率

噪声可以用任意频率生成，而我目前只选用了一种频率。咱们来看看频率会产生什么影响 —— 试着拖动滑块，就能看到不同频率下的效果了：

三种频率的对比

第一种：

elevation[y][x] = noise(1.48 * nx, 1.48 * ny);

elevation[y][x] = noise(3.90 * nx, 3.90 * ny);

elevation[y][x] = noise(5.88 * nx, 5.88 * ny);

仅仅出现了地图缩放。乍一看这并不怎么实用，但事实上它很有用。

elevation[y][x] = noise(frequency * nx, frequency * ny);

如果你能联想到波长（wavelength），即频率的倒数，它有时就能很有用。频率的单位是每单位距离的振荡次数。将频率加倍，会使所有事物的尺寸减半。波长则是每次振荡所对应的距离，用像素、方块、米等单位来衡量。将波长加倍，会使所有事物的尺寸加倍。波长和频率之间的关系是：波长 = 地图大小 / 频率。

elevation[y][x] = noise(x / wavelength, y / wavelength);

在另一篇教程中，我解释了相关概念：频率，波长，波幅，频程，粉红噪声、蓝色噪声和白噪声等等。

频程

为了让高度图更有趣，我们会在不同频率下添加噪声：

elevation[y][x] = 1 * noise(1 * nx, 1 * ny)
                + 0.5 * noise(2 * nx, 2 * ny)
                + 0.25 * noise(4 * nx, 4 * ny);

让我们把大的低频山丘和小的高频山丘混合在同一张地图中。移动滑块可以往其中添加更小的山丘：

现在看起来就更像我们想要的分形地形了！我们现在可以得到山丘和崎岖的山脉，但仍然没有平坦的山谷。要实现这一点，我们还需要其他方法。

不过这里存在一个潜在问题。由于噪声值（noise）的范围是 0 到 1，所以 1 * noise() + 0.5 * noise() + 0.25 * noise() 这个求和结果的范围会是 0 到 1.75。其中，[1, 0.5, 0.25] 这组数字被称为波幅。最简单的解决方法是将求和结果除以波幅的总和。

e = 1 * noise(1 * nx, 1 * ny)
	+ 0.5 * noise(2 * nx, 2 * ny)
	+ 0.25 * noise(4 * nx, 4 * ny);
elevation[y][x] = e / (1 + 0.5 + 0.25);

在实际操作中，你可能需要通过实验来找到最佳的除数。尽管波幅总和能确保海拔（elevation）保持在 0-1 的范围内，但海拔的分布方式可能并非你所期望的。

波幅（amplitude）通常被设为一个数组 [1, 1/2, 1/4, 1/8, 1/16, …]，其中每个波幅都是前一个的二分之一。这个比例被称为增益（gain）或持续度（persistence）。不过，我们并不局限于使用固定的比例。我在本页的许多示例中使用的是 [1, 1/2, 1/3, 1/4, 1/5] 这样的波幅，这能比传统的设置带来更多的细节。波幅也可以动态计算，例如可以根据前一次噪声的结果（比如第一倍频程的噪声可以影响第二倍频程的波幅），也可以通过一个独立的噪声场，或者利用玩家或模拟数据来决定。

另一种可能的问题是：当使用 noise(1 * nx, 1 * ny) 、 noise(2 * nx, 2 * ny) 和 noise(4 * nx, 4 * ny) 时，如果 nx 和 ny 接近 0，会发生什么？这些噪声值之间是有关联的。为了获得最佳效果，我们希望这些值是相互独立的。如果你的噪声库支持设置种子，可以为每个频程设置不同的随机数种子。如果噪声函数库不支持随机种子，可以为每个频程添加一个偏移量，如 noise(1 * nx, 1 * ny) 、 noise(2 * nx + 5.3, 2 * ny + 9.1) 和 noise(4 * nx + 17.8, 4 * ny + 23.5) 。这样，每个频程就会从噪声空间的不同部分进行采样，因此它们是独立的，而不是相关的。还有另一个可能得问题：这些噪声值有可能会在相同的方向上整齐排列，这有时可能会导致明显的人工痕迹，尤其是使用 Perlin 噪声时。为避免这种情况，可以为一些频程的输出数值添加旋转角度，也可以改用 Simplex 噪声。

再分布

噪声函数返回的是介于 0 和 1 之间的数值。为了这制造平坦的山谷，我们可以取海拔的幂函数。移动滑块来尝试不同的指数：

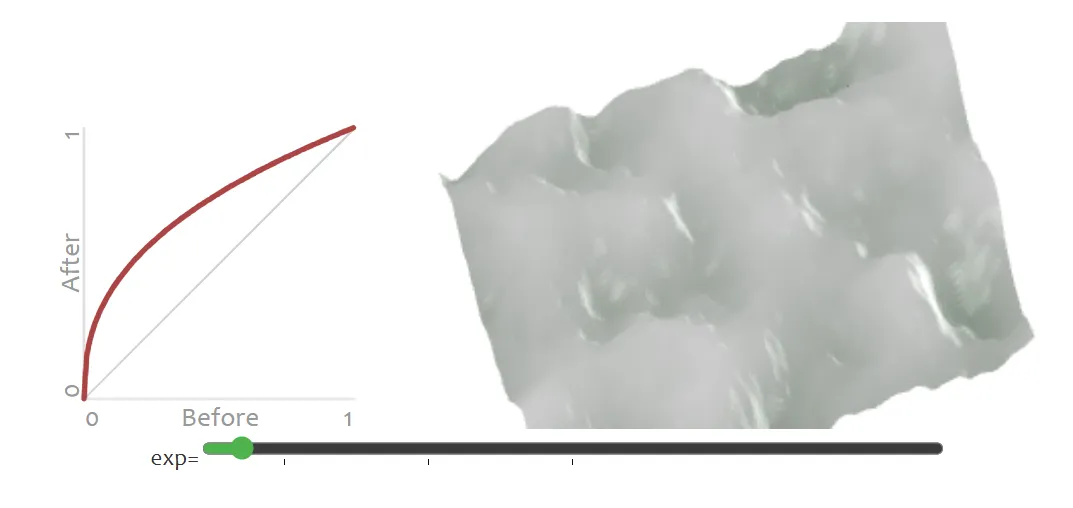
e = 1 * noise(1 * nx, 1 * ny)
  + 0.5 * noise(2 * nx, 2 * ny)
  + 0.25 * noise(4 * nx, 4 * ny);

e = e / (1 + 0.5 + 0.25);
elevation[y][x] = Math.pow(e, 0.40);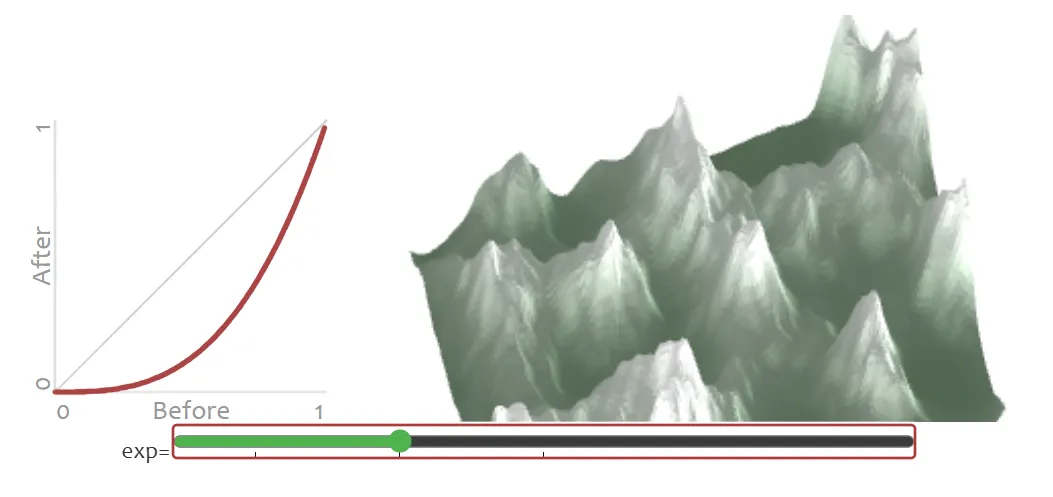

e = 1 * noise(1 * nx, 1 * ny)
  + 0.5 * noise(2 * nx, 2 * ny)
  + 0.25 * noise(4 * nx, 4 * ny);

e = e / (1 + 0.5 + 0.25);
elevation[y][x] = Math.pow(e, 3.00);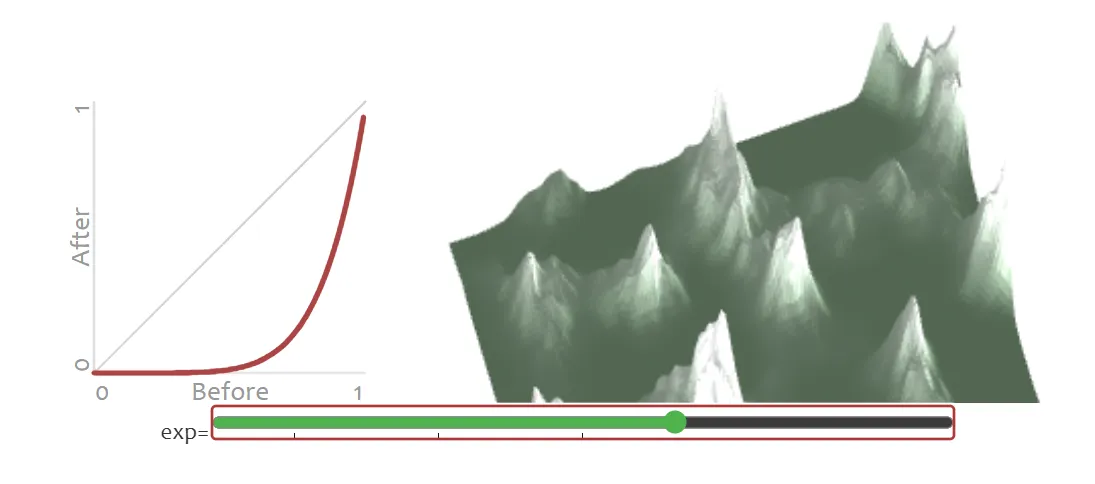

e = 1 * noise(1 * nx, 1 * ny)
  + 0.5 * noise(2 * nx, 2 * ny)
  + 0.25 * noise(4 * nx, 4 * ny);

e = e / (1 + 0.5 + 0.25);
elevation[y][x] = Math.pow(e, 6.28);

指数取较大值时，海拔居中的位置会下沉为谷地；指数取较小值时，海拔居中的位置则会隆起为山峰。我们的目标是让这些位置下沉。我采用幂函数是因为它足够简单，但你也可以使用任何你想要使用的曲线函数。

实践中，使用 Math.pow(e * fudge_factor, exponent) 的效果可能会更好，其中 fudge_factor 是一个接近 1 的数值。在上述样例中，我取其为 1.2。你也可尝试其他数值，看看哪个效果最好。

幂函数 pow() 并非唯一可以用来重塑海拔图形状的方法，还有许多别的函数可以尝试。也不局限于必须使用数学函数，你可以考虑自己绘制曲线，类似图片编辑软件中的曲线工具那样。

现在，我们已经获得了一张理想的高度图，让我们来为它添加一些生物群系吧！